Abstract: Das gemeinsame Lernen an einem gemeinsamen Gegenstand stellt ein Ideal des inklusiven Mathematikunterrichts dar, soll dieses doch ein gemeinsames Lernen von Schülerinnen und Schülern mit sehr heterogenen Lernvoraussetzungen im Sinne eines von- und miteinander Lernens ermöglichen. Dabei stellt sich die Frage, inwieweit Lernende in Phasen des gemeinsamen Lernens an einem gemeinsamen Gegenstand miteinander kooperieren und tatsächlich gemeinsam lernen. Dazu werden im Artikel anhand von exemplarischen Szenen kollektive Arbeitsprozesse diskutiert und sozial-kommunikative Interaktionsstrukturen rekonstruiert.
Stichworte: gemeinsames Lernen an einem gemeinsamen Gegenstand, inklusiver Mathematikunterricht, sozial-kommunikative Interaktionsstrukturen
Inhaltsverzeichnis
Inhaltsverzeichnis
Ziel des inklusiven Mathematikunterrichts ist, alle Schülerinnen und Schüler unabhängig von individuellen Lernvoraussetzungen einzubeziehen und die Entwicklung zentraler mathematischer Kompetenzen zu unterstützen. Dazu muss sich der Unterricht gegenüber den jeweiligen Kompetenzen und Bedürfnissen jedes Einzelnen öffnen. Gleichzeitig besteht eine zentrale Aufgabe darin, die Heterogenität der Lerngruppe als Chance (Boban & Hinz 2003; Prengel 2006) für produktive, gemeinsame Lernprozesse aufzufassen. Folglich spielt im inklusiven Unterricht die Förderung fachlicher Lernprozesse aller Lernenden eine zentrale Rolle (Carle 2017). Damit kombiniert der Begriff des gemeinsamen Lernens sowohl eine Individualisierung des Lernens als auch eine fachliche Gemeinsamkeit.
Damit diese hohen normativen Ansprüche erfüllt werden können, müssen bei der didaktischen Gestaltung eines inklusiven Mathematikunterrichts besonders drei zentrale Aspekte berücksichtigt werden: (1) Umsetzung unterrichtsintegrierter (sonder-)pädagogischer Unterstützungsmaßnahmen; (2) Berücksichtigung der individuellen Fähigkeiten und Ermöglichung eines Lernens auf unterschiedlichen Niveaus; (3) Initiierung von möglichst vielen gemeinsamen Lernphasen (Häsel-Weide 2017; vgl. auch Gersten et al. 2009; Montague 2011). Um dem Ziel eines gemeinsamen (Mathematik-)Lernens gerecht zu werden, sollte der Unterricht möglichst viele gemeinsame Lernsituationen umfassen. Diesbezüglich können nach Wocken (1998) verschiedene, idealtypische Lernsituationen unterschieden werden:
Insgesamt offenbaren die Lernsituationen verschiedene Möglichkeiten, um sich in dem Spannungsfeld zwischen Individualisierung und Gemeinsamkeit (vgl. Häsel-Weide 2017; Häsel-Weide & Nührenbörger 2017; Peter-Koop 2016) zu bewegen. Beide Aspekte sind gleichermaßen für die Ermöglichung inklusiver Prozesse erforderlich. Dabei variieren die Lernsituationen nicht nur von Unterrichtsstunde zu Unterrichtsstunde, sondern können sich ebenfalls innerhalb einer Stunde ändern. So ist es beispielsweise denkbar, dass Lernende zunächst individuell Aufgaben koexistent oder informell subsidiär auf verschiedenen Niveaus bearbeiten und zu eigenen Ergebnissen kommen. In einer folgenden Arbeitsphase stellen sich die Lernenden ihre Arbeitsergebnisse und -prozesse gegenseitig vor (solidarische Lernsituation). Das gemeinsame Ziel bezieht sich hierbei auf einen gemeinsamen Lerngegenstand.
Gemeinsames, kooperatives Lernen an einem gemeinsamen Gegenstand
Ein solches kooperatives Lernen an einem gemeinsamen (Lern-)Gegenstand erfährt eine hohe Wertschätzung (Lütje-Klose & Miller 2015; Moser Opitz 2014) und wird als didaktisches Modell vielfach sowohl in der theoretischen Diskussion als auch in der praktischen Umsetzung eines inklusiven Mathematikunterrichts aufgegriffen (u. a. Fetzer 2016; Hähn 2021; Häsel-Weide 2017; Häsel-Weide & Nührenbörger 2017; Korten 2020; Schöttler & Häsel-Weide 2017).
Die Idee des Lernens an einem gemeinsamen Gegenstand wurde von Feuser (1989) in seiner allgemeinen, integrativen Pädagogik erarbeitet und meint, dass „alle Kinder in Kooperation miteinander auf ihrem jeweiligen Entwicklungsniveau und mittels ihrer momentanen Denk- und Handlungskompetenzen an und mit einem gemeinsamen Gegenstand lernen und arbeiten“ (S. 22). Ein gemeinsames Lernen ist durch ein Miteinander-Lernen geprägt.
Eine ähnliche Idee beschreibt Freudenthal (1974) explizit für den Mathematikunterricht, wobei er sich auf die Heterogenität einer „normalen“ Schulklasse bezieht. So formuliert er die Idee eines Lernens „miteinander am gleichen Gegenstand auf verschiedenen Stufen“ (S. 166) und fordert ebenfalls, dass alle Lernenden am gleichen Gegenstand arbeiten sollen, aber jeder auf seiner Stufe des Verständnisses. Dabei bezieht sich ein gleicher Gegenstand nicht auf Lernprozesse am „gleichen Stoffe“ (Freudenthal 1974, S. 166), sondern im engeren Sinne auf einen gleichen Fachgegenstand, an dem die Lernenden auf unterschiedlichen Bearbeitungsniveaus arbeiten. Durch die Zusammenarbeit sollen alle Lernenden ihre Kompetenzen erweitern, indem sich Leistungsschwächere an den Fähigkeiten der anderen orientieren und Leistungsstärkere durch einen reflexiven Blick auf die niedrigere Stufe neue Einsichten bekommen (Freudenthal 1974, S. 167).
Obwohl Feuser und Freudenthal die Idee beschreiben, dass sich Lernende auf unterschiedlichen Bearbeitungsniveaus nicht neben-, sondern miteinander mit denselben Prozessen und Phänomenen auseinandersetzen, lassen sich dennoch Unterschiede insbesondere im Hinblick auf den Gegenstand erkennen. Während Feuser den gemeinsamen Gegenstand weiter fasst, da er nicht auf den sachlichen Inhalt, sondern auf Kompetenzen fokussiert, die die Lernenden erwerben sollen, und das Lernen an einem gemeinsamen Gegenstand nur in Projektarbeit umgesetzt sieht (Feuser 1989), bezieht sich Freudenthals Verständnis des Gegenstandes auf einen vielschichtigen, aber logisch zusammenhängenden Themenkomplex entlang eines für alle gemeinsamen Fachgegenstandes. In diesem Beitrag wird der „gemeinsame Gegenstand“ in diesem engeren Sinne verstanden.
Das gemeinsame Lernen an einem gemeinsamen Gegenstand ähnelt der von Wocken (1998) beschriebenen solidarischen Lernsituation, auch wenn für Wocken das „didaktische Paradestück“ solidarischer Lernsituationen arbeitsteilige Vorhaben und Projekte sind (S. 49). Dies widerspricht jedoch zum Teil dem diesem Beitrag zugrunde gelegten Verständnis eines gemeinsamen Lernens an einem gemeinsamen Gegenstand, da hierbei die Lernenden gemeinschaftlich entlang eines gleichen Fachgegenstandes arbeiten.
Durch die Implementierung eines gemeinsamen Gegenstandes können alle Lernenden sowohl individuell als auch von- und miteinander lernen. Das Lernen an einem gemeinsamen Gegenstand bezieht sich nicht auf ein zielgleiches Lernen im Gleichschritt. Vielmehr sollen alle Schülerinnen und Schüler am gleichen Inhalt, aber auf unterschiedlichen Niveaus gemäß ihrem individuellen Tempo und auf eigenen Wegen lernen. Dabei verfolgen sie unterschiedliche Ziele, die sich an dem gemeinsamen Gegenstand orientieren. Um gemeinsame Lernprozesse zu fördern, wird ein zieldifferentes, gemeinsames Lernangebot benötigt, in dem der gemeinsame Gegenstand im Zentrum steht. Aus mathematikdidaktischer Sicht stellt sich vor allem die Frage, wie gleichzeitig über die Arbeit an einem Gegenstand gemeinsame Zielsetzungen verfolgt und zieldifferentes Arbeiten ermöglicht werden können, ohne den fachlichen Anspruch aufzugeben.
Da weder Feuser noch Freudenthal ihre Überlegungen so ausgearbeitet haben, dass diese direkt auf den inklusiven Mathematikunterricht übertragen werden können, bedarf es einer Konkretisierung, wie die Idee im inklusiven Mathematikunterricht umgesetzt werden kann. In dem Zusammenhang lassen sich auf der Basis verschiedener mathematikdidaktischer Überlegungen (Fetzer 2016; Häsel-Weide 2017; Häsel-Weide & Nührenbörger 2015; 2017; Moser Opitz 2014; Scherer 2017; Schindler 2017; Schöttler & Häsel-Weide 2017; Transchel 2019) drei Merkmale eines gemeinsamen Lernens an einem gemeinsamen Gegenstand unterscheiden:
Als besonders geeignet für gemeinsame Gegenstände erweisen sich Unterrichtsinhalte, die den fundamentalen Ideen der Mathematik (Winter 2001; Wittmann 1998) entsprechen. Hierbei handelt es sich um wesentliche und unverzichtbare Inhalte, welche sich durch die gesamte Mathematik ziehen und deren Erarbeitung durch eine wiederkehrende Beschäftigung auf immer höherem Niveau mit steigendem Abstraktionsgrad erfolgt (Krauthausen 2018). Dadurch werden Inhalte auf unterschiedlichen Bearbeitungsniveaus erwerbbar. Beispielsweise können alle Lernenden an der fundamentalen Idee des Stellenwertsystems arbeiten, indem manche Lernende mithilfe von Material erste, grundlegende Erfahrungen zum Aufbau natürlicher Zahlen sammeln, während andere ihr Wissen zum Aufbau natürlicher Zahlen auf Dezimalbrüche übertragen.
Die Orientierung an fundamentalen Ideen ist für den inklusiven Mathematikunterricht bedeutsam, da so für alle Schülerinnen und Schüler zentrale Lerninhalte ausgewählt werden, mit denen sich alle beschäftigen (inhaltliche Gemeinsamkeit).
Für die Gestaltung mathematischer Lernprozesse entlang eines gemeinsamen Gegenstandes werden Aufgabenformate benötigt, die allen Schülerinnen und Schülern differenzsensible, verstehensorientierte Tätigkeiten auf dem jeweiligen Niveau ermöglichen. Dabei bildet die fundamentale Idee den fachlichen Rahmen. Wichtig ist, dass alle Lernenden selbst komplexe Strukturen erkunden, um ein inhaltliches Verständnis aufzubauen. Dies ist für langfristig erfolgreiches mathematisches Lernen wichtig, da „Komplexität [...] für das Verständnis nicht erschwerend, sondern hilfreich [ist], weil in der ganzen Struktur mehr Bedeutung, mehr Sinn, mehr Information für Lösungen enthalten ist als in isolierten Teilaufgaben“ (Hengartner 1992, S. 15ff). Dies bedeutet, dass Inhalte nicht didaktisch in kleine Teile zerlegt und so die Anforderungen inhaltlich eingeschränkt werden dürfen (Krauthausen 2018, S. 228).
Gleichzeitig müssen die Zugänge zum gemeinsamen Gegenstand so gestaltet werden, dass sich alle Schülerinnen und Schüler inhaltlich aktiv einbringen können. Dazu muss das Lernangebot u. a. eine niedrige Einstiegsschwelle auf einer basalen Ebene bieten, damit grundlegende Kompetenzen erworben werden können und für fortgeschrittenere Lernende anspruchsvollere, weiterführende Aufgaben beinhalten, um vorhandene Kompetenzen zu vertiefen. Differenzsensible Angebote meinen also, dass Inhalte unter Beachtung individueller Kompetenzen und Lernvoraussetzungen so aufbereitet werden, dass vielfältige fachliche Zugänge genutzt werden können. Diesbezüglich bieten sich „natürlich differenzierende“ (Krauthausen & Scherer 2014) oder „struktur-analoge“ Aufgaben (Nührenbörger & Verboom 2005) an, welche ein Lernen auf unterschiedlichen Niveaus und auf verschiedenen Wegen entlang des gemeinsamen Gegenstandes ermöglichen; gleichzeitig können mathematische Strukturen erkundet werden.
Besonders für den inklusiven Mathematikunterricht besteht aufgrund der großen Heterogenität an Kompetenzen die Hoffnung, dass die Vielfalt zu einer breiten Spanne an Vorgehensweisen und Deutungen führt, welche innerhalb gemeinsamer Austauschphasen ausgehandelt werden, wovon alle Lernenden profitieren (Häsel-Weide & Nührenbörger 2015; Häsel-Weide 2016). Dabei ist die Forderung nach Kooperation und Kommunikation aus fachlichen Gründen von großer Bedeutung, da der Erwerb neuen mathematischen Wissens in sozial-interaktive Prozesse integriert ist: in Gespräche über Vorstellungen und Vorgehensweisen, in die Aushandlung verschiedener Ansichten und durch Anregungen anderer (Steinbring & Nührenbörger 2010). Dementsprechend kann kooperatives Lernen ein gemeinsames, fachliches Lernen ermöglichen (Häsel-Weide 2017; Schöttler & Häsel-Weide 2017; Transchel 2019).
Damit sich Lernende über Entdeckungen, Lösungsprodukte, -ideen und -wege austauschen und zu gemeinsamen Erkenntnissen kommen können, sollten sie durch ein methodisches Setting gezielt dazu angeregt werden (Häsel-Weide 2016; Schöttler & Häsel-Weide 2017). Durch die Gestaltung kooperativer Tätigkeiten, die einerseits die Kriterien kooperativen Lernens (positive Interdependenz, individuelle und Gruppen-Verantwortlichkeit, Face-to-face-Kommunikation, Interpersonale Fähigkeiten und Reflexion der Gruppenprozesse; Borsch 2010; Johnson et al. 2005) erfüllen und andererseits einen offenen Austausch über den gemeinsamen Gegenstand sowie ein zieldifferentes Vorgehen ermöglichen, kann ein fachlicher Austausch initiiert werden.
Allerdings bleibt die Spanne zwischen den individuellen Kompetenzen und Einsichten der Lernenden zum Gegenstand und dem, was im Sinne einer lernförderlichen Differenz ein gemeinsames Lernen unterstützt und nicht kontraproduktiv wirkt, die größte Herausforderung. Die Heterogenität kann in kooperativen Settings produktiv wirken, d. h., gerade die Auseinandersetzung mit den Gedanken anderer bietet die Chance, die Vielfalt als Lernanlass zu nutzen. Sind die Differenzen jedoch zu groß und können Lernende Gedanken anderer nicht nachvollziehen, kann sich Vielfalt negativ auf die Kooperation auswirken (Webb 1989).
Insgesamt scheinen die Merkmale geeignet zu sein, um ein gemeinsames Lernen an einem gemeinsamen Gegenstand zu initiieren. Allerdings kann nicht garantiert werden, dass die Schülerinnen und Schüler die Lernangebote zum individuellen und gemeinsamen Lernen auch wirklich nutzen und gehaltvoll über Mathematik sprechen. So ist es möglich, dass das gleiche Lernangebot manche Lernenden anregt, über mathematische Inhalte zu kommunizieren und zu gemeinsamen Ergebnissen zu kommen, während andere die Aufgaben nicht gemeinsam bearbeiten und so nicht von- und miteinander lernen. Deshalb ist es neben einer theoretischen Beschreibung dieser Lernsituation wichtig, empirisch zu untersuchen, ob und inwieweit der normative Anspruch vor dem Hintergrund der breiten Spanne an möglichen Bearbeitungen und individuellen Deutungen tatsächlich erfüllt wird: In welchem Maß führt eine gemeinsame Aufgabe zu einem gemeinsamen Lernen? Welche Aushandlungsprozesse lassen sich innerhalb intendierter Austauschphasen rekonstruieren? Wie handeln Lernende mit unterschiedlichen Lernvoraussetzungen verschiedene Ideen aus?
Dazu sollen in diesem Artikel Interaktionsprozesse zwischen Schülerinnen und Schülern beim gemeinsamen Lernen an einem gemeinsamen Gegenstand fokussiert und auf der Grundlage von empirischen Daten diskutiert werden. Dabei sollen nicht gelungene oder nicht-gelungene Kooperationen erforscht werden; stattdessen geht es darum, Erkenntnisse hinsichtlich der Strukturierungsprozesse der Unterrichtsabläufe zu gewinnen. Konkret ergibt sich folgende Frage:
Der Fokus dieses Artikels liegt auf den während des fachlichen Austauschs emergierenden Interaktionsstrukturen und Intention ist die Generierung neuer Theorien zu Interaktionsprozessen im inklusiven Mathematikunterricht. Dazu wird eine deskriptive Perspektive auf Schüler-Schüler-Interaktionen eingenommen. Dies ist mit dem Ziel verbunden, die beschriebene Lernsituation des gemeinsamen Lernens an einem gemeinsamen Gegenstand als empirisches Phänomen zu bestimmen. Zur Rekonstruktion der Interaktionsprozesse sind Methoden der interpretativen Unterrichtsforschung geeignet.
In der Mathematikdidaktik lassen sich unter der Bezeichnung interpretative Unterrichtsforschung rekonstruktiv-interpretative Verfahren der Lehr-Lern-Forschung zusammenfassen (Schreiber et al. 2015). Ihr Forschungsfokus liegt auf den in unterrichtlichen Interaktionen ständig neu erzeugten Deutungen und Deutungszuschreibungen. Diesem Gedankengang folgend werden Deutungsaushandlungen als ein dynamisches und sich wechselseitig beeinflussendes, situationsbezogenes Interpretieren von mathematischen Beiträgen aufgefasst (Jungwirth 2003; Krummheuer & Brandt 2001; Naujok 2000; Schreiber et al. 2015). Interpretative Mathematikdidaktik befasst sich daher u. a. „[...] mit den Lehr- und Lernprozessen selbst, also mit fachbezogenen unterrichtlichen Interaktionen, Beteiligungsstrukturen und kollektiven Themen – und Interessenentwicklungen“ (Jungwirth 2003, S. 190).
Zur Rekonstruktion der Interaktionsprozesse wurde die systematisch-extensionale Interpretation als Methode der interpretativen Unterrichtsforschung genutzt (Beck & Maier 1994). Die systematisch-extensionale Interpretation bezieht sich auf eine qualitative Analyse einzelner Phänomene und geht datengeleitet vor, die Theorie wird also aus dem Text heraus entwickelt (Beck & Maier 1994); im konkreten Fall wurden jeweils zwei Schülerinnen und Schüler bei der gemeinsamen Arbeit an einem gemeinsamen Gegenstand videografiert und die Szenen transkribiert. Im Anschluss wurden die Szenen hinsichtlich der emergierenden Interaktionsprozesse nach folgenden Schritten analysiert:
Ziel dieser Analysen ist die Generierung neuer, empirisch basierter Theorieelemente zu Interaktionsprozessen im inklusiven Mathematikunterricht. Dazu wurde die komparative Analyse (Krummheuer & Brandt 2001) genutzt, mit der innerhalb eines methodischen Vorgehens Gemeinsamkeiten und Unterschiede in Interaktionsprozessen unterschiedlicher Paare beschrieben werden können. Durch einen Vergleich von möglichst kontrastreichen Interaktionen gestattet die Komparation an einzelnen Fällen ein kontrolliertes Vorgehen zur Entwicklung neuer Theorieelemente (Krummheuer & Brandt 2001). „Der Vergleich und die Kontrastierung von Fällen ist [...] eine notwendige Voraussetzung, um zu einer validen und methodisch kontrollierten Beschreibung und Erklärung sozialer Strukturen zu gelangen“ (Kelle & Kluge 2010, S. 11). Durch ein systematisches Vergleichen und eine gezielte Auswahl kontrastreicher Beispielszenen konnten theoriegeleitet besondere Phänomene von Interaktionsprozessen herausgefiltert werden. Auf diese Weise soll ein breiterer Blick auf die fachliche Gemeinsamkeit eröffnet werden.
In diesem Zusammenhang wurden mithilfe von abduktiven Schlüssen (Krummheuer & Brandt 2001, S. 80) Hypothesen generiert, die gleichzeitig auf der Analyse des empirischen Datenmaterials (transkribierte Szenen) sowie auf vorhandenen Forschungen beruhen (insbesondere Naujok (2000) und Hackbarth (2017); s. u.). Dadurch konnten sozial-kommunikative Interaktionsstrukturen abgeleitet werden.
Als Ausgangspunkt der Studie wurden Lernangebote entwickelt, die den skizzierten, mathematikdidaktischen Kriterien eines gemeinsamen Lernens an einem gemeinsamen Gegenstand genügen. Im Rahmen der konzipierten Lernangebote arbeiten alle Lernenden an der fundamentalen Idee des Stellenwertsystems, aber auf unterschiedlichen Stufen des Verständnisses. Während Leistungsstärkere bereits zuvor ein Verständnis des Aufbaus von Zahlen bis 1.000.000 aufgebaut haben und dieses auf Dezimalbrüche erweitern, arbeiten Lernende mit sonderpädagogischem Förderbedarf im Bereich Lernen im Zahlenraum bis 1.000. Diese Lernenden sind noch dabei, die wesentlichen Eigenschaften des Dezimalsystems im Tausenderraum zu erarbeiten. Trotz unterschiedlicher Lernvoraussetzungen haben Lernende mit und ohne sonderpädagogischen Förderbedarf die Gelegenheit, sich gemeinsam über den Aufbau von Zahlen auszutauschen, um so individuelle Einsichten in zentrale Eigenschaften des Dezimalsystems zu vertiefen. Die entwickelten Lernangebote wurden in verschiedenen Gesamtschulen mit gemeinsamem Unterricht erprobt und dabei der Unterricht videografiert.
Interaktionsprozesse innerhalb gemeinsamer Tätigkeiten an einem gemeinsamen Gegenstand im inklusiven Mathematikunterricht sind aus interaktionistischer Perspektive bislang noch nicht erörtert worden. Stattdessen wurden in verschiedenen Arbeiten, wie z. B. durch Naujok (2000) oder speziell für den inklusiven Unterricht von Hackbarth (2017), soziale Strukturen in breiter gefassten Schülerkooperationen untersucht und unterschiedliche Kooperationstypen herausgearbeitet.
In ihrer Studie untersuchte Naujok (2000) Kooperationen im Kontext von Wochenplanunterricht, in dem Lernende in relativ frei zu gestaltenden Handlungsspielräumen zusammenarbeiteten. Folglich liegt der Studie ein breites Verständnis von Kooperation als „jede Art von aufgabenbezogener Interaktion“ (Naujok 2000, S. 12) zugrunde. Dabei unterscheidet Naujok (2000, S. 171ff) die Kooperationstypen „Nebeneinanderher-Arbeiten“, „Helfen“ und „Kollaborieren“.
Hackbarth (2017) erforschte spontan auftretende, „aufgabenbezogene Schülerinteraktionen“ (S. 81) während gemeinsamer Aufgabenbearbeitungen, wobei die Studie ebenfalls auf einem weiten Kooperationsbegriff aufbaut. Als Ergebnis konnte Hackbarth (2017) die Typen „Konkurrenz“, „Instruktion“ und „Ko-Konstruktion“ rekonstruieren.
Da in diesem Beitrag Interaktionsprozesse in speziell arrangierten und methodisch strukturierten, kooperativen Phasen des gemeinsamen Lernens an einem gemeinsamen Gegenstand fokussiert werden – mit einem engen Begriffsverständnis von gemeinsamen Gegenständen (s. o.) – liegt hier ein engerer Kooperationsbegriff zugrunde als den Arbeiten von Hackbarth (2017) und Naujok (2000).
Zusätzlich gibt es die bereits oben skizzierten gemeinsamen Lernsituationen von Wocken (1998), die typische Situationen eines inklusiven (Mathematik-)Unterrichts beschreiben. Diese sind jedoch weder empirisch hergeleitet, sondern theoretisch beschrieben, noch beziehen sie sich nicht explizit auf Situationen, in denen Lernende gemeinsam an einem gemeinsamen Gegenstand lernen; stattdessen umfassen diese z. B. auch Situationen, in denen keine gemeinsame Tätigkeit intendiert ist und die Lernenden verschiedene Aufgaben bearbeiten.
Sozial-kommunikative Interaktionsstrukturen
Als Ergebnis der Analysen konnten in einem abduktiven Vorgehen drei sozial-kommunikative Interaktionsstrukturen innerhalb intendierter gemeinsamer Tätigkeiten an einem gemeinsamen Gegenstand im inklusiven Mathematikunterricht rekonstruiert werden. Die herausgearbeiteten Interaktionsstrukturen werden im Folgenden anhand von Einzelfallbeispielen erläutert, die typische Merkmale der zugrunde liegenden Prozesse aufzeigen (vgl. Beck & Maier 1994). Die zentrale Wirkkraft von Einzelfallbeispielen liegt darin begründet, „[…] die Komplexität eines Falls möglichst umfassend und detailliert“ (Bortz & Döring 2006, S. 323) abzubilden.
|
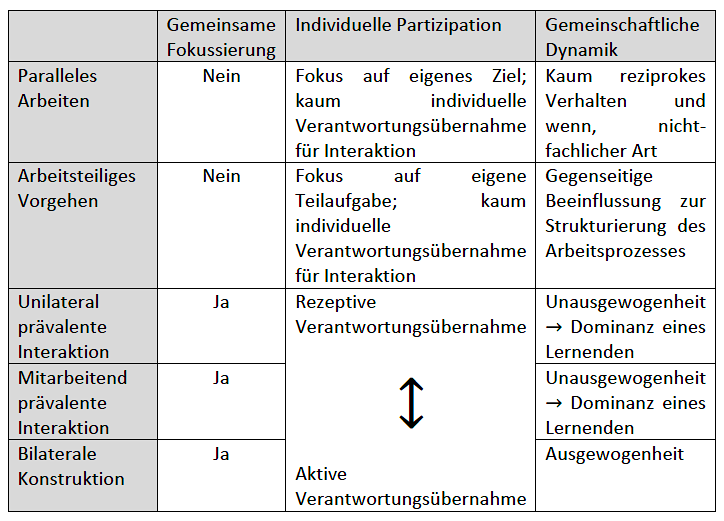
Abb. 1: Sozial-kommunikative Interaktionsstrukturen
Die sozial-kommunikativen Interaktionsstrukturen lassen sich über (1) die individuelle Partizipation an der gemeinsamen Tätigkeit, (2) die gemeinschaftliche Dynamik der Kooperation sowie (3) die gemeinsame Fokussierung auf die Aufgabe beschreiben und voneinander differenzieren.
Die individuelle Partizipation steht in Relation zu den Rollen, die die Lernenden im gemeinsamen Bearbeitungsprozess einnehmen und wie sie sich einbringen. Die individuelle Partizipation wirkt sich maßgeblich auf die gemeinschaftliche Dynamik aus, dennoch stellt diese eine eigene Dimension dar. Hierbei wird untersucht, wie die Partnerinnen und Partner miteinander interagieren, Lösungsideen (kollektiv) aushandeln und sich gegenseitig beeinflussen.
Während intendierter gemeinsamer Tätigkeiten sprechen die Paare nicht nur über mathematische Inhalte; stattdessen kann sich der Fokus auf verschiedene Bereiche beziehen, die sich im Interaktionsverlauf dynamisch ändern: Fachliches, Organisatorisches oder Soziales. Zudem kann es sein, dass Paare nicht miteinander kommunizieren. Deshalb bezieht sich die dritte Dimension auf die thematische Fokussierung: Fassen die Lernenden die Aufgabe als eine gemeinsame auf, die sie zusammen bearbeiten, oder arbeiten sie getrennt? Um mit der gemeinsamen Tätigkeit zu beginnen, ist ein Konvergieren der Aufmerksamkeiten auf die gemeinsame Tätigkeit sowie die individuelle Bereitschaft, sich auf die Aufgabe einzulassen, zentral.
Durch die Beschreibung der Interaktionsstrukturen über die drei Dimensionen liegt der Fokus auf der individuellen Beteiligung am (gemeinsamen) Aushandlungsprozess und nicht auf den jeweiligen kognitiven Kompetenzen und Fähigkeiten.
Fachlich separate Arbeitsprozesse
Innerhalb von fachlich separaten Arbeitsprozessen bearbeiten die Paare ihre Aufgaben nicht gemeinsam, sondern nebeneinander; sie fokussieren sich also nicht auf die gemeinsame Aufgabe. Austausch findet, wenn überhaupt, beiläufig statt und dann interagieren sie auf einer sozialen oder organisatorischen Ebene, z. B. um den Arbeitsprozess zu strukturieren. In seltenen Fällen tauschen sich die Paare fachlich über Fakten aus, jedoch ohne kollektiv Lösungsideen auszuhandeln. Dementsprechend bezieht sich die gemeinschaftliche Dynamik auf nicht-fachliche Aspekte.
Je nach Intensität des nicht-fachlichen Austauschs und der Aufteilung des Arbeitsprozesses lassen sich zwei Formen fachlich separater Arbeitsprozesse unterscheiden.
Beide Lernende bearbeiten individuell die Aufgaben und verfolgen eigene Ideen, aber kein gemeinsames Ziel. Gespräche finden kaum statt und wenn, sind diese temporär und es stehen nicht-fachliche Inhalte im Fokus.
Beispiel: Ekin und Taki sollen zwei zuvor in Einzelarbeit beschriftete Arbeitsblätter im Hinblick auf Gemeinsamkeiten und Unterschiede vergleichen:
Taki |
Das geht gar nicht. Der hat anders. |
Ekin |
Ja, das soll auch anders sein. |
Taki |
Na und? Wir haben nichts gleich. |
Ekin |
Wir haben bestimmt etwas gleich, lass uns doch gucken. Wir finden bestimmt was gleich ist oder nicht gleich ist. |
Taki |
Nein, lass mich. (notiert: ‚Mein Partner hat andere Zahlen und andere Blatt‘) |
Ekin |
(20 Sekunden Pause) Taki, jetzt zeig doch mal. Was schreibst du? (nimmt sich Takis Zettel und liest) ‚Mein Partner hat andere Zahlen und andere Blatt.‘ Wir müssen das vergleichen. Wir haben bestimmt was gleich. |
Taki |
Nein, ich mache das jetzt alleine. Dann bin ich eh schneller, wenn ich nicht auf dich warten muss. (blickt kurz auf Ekins Arbeitsblatt und notiert: ‚Ich habe 300, mein Partner hat 300000. 3 Nullen sind mehr‘) |
Ekin |
Aber wir müssen das doch zusammen machen. |
In der Interaktion wird deutlich, dass die beiden nicht mit der gemeinsamen Tätigkeit beginnen. Dies scheint insbesondere an Taki zu liegen, der kein Interesse an der Interaktion zeigt. Obwohl Ekin Taki direkt anspricht, Takis Notizen sehen möchte sowie die Verbindlichkeit der gemeinsamen Aufgabe betont (‚wir müssen das vergleichen‘) und so eine generelle Kooperationsbereitschaft signalisiert, ist aufgrund von Takis ablehnender Haltung keine gemeinsame Vergleichsphase möglich.
Für Taki scheint die Zusammenarbeit aus zwei Gründen nicht gewinnbringend zu sein: Einerseits geht er anscheinend davon aus, dass ein Vergleich inhaltlich wenig Sinn macht, da sie verschiedene Arbeitsblätter erhalten haben. So verbalisiert er zunächst, dass sie ‚nichts gleich‘ haben, erkennt jedoch nach einem Blick auf Ekins Arbeitsblatt Gemeinsamkeiten und Unterschiede. Andererseits zeigt er keine Wertschätzung gegenüber der gemeinsamen Tätigkeit, da er äußert, die Aufgabe alleine schneller lösen zu können. In dieser Äußerung zeigt sich eine Wettbewerbssituation (Hackbarth 2017, S. 116ff), indem sich Taki in Konkurrenz zu Ekin setzt und die Aufgabe schneller lösen möchte, sodass eine Strittigkeit nicht-fachlicher Art auftritt. Obwohl Ekin wiederholt darauf hinweist, dass der Vergleich ihre gemeinsame Aufgabe ist, arbeiten schließlich beide individuell und kommen zu verschiedenen Lösungen, wodurch sie nicht gemeinsam lernen. In der Szene hat das Gesprächsthema einen organisatorischen Charakter, obwohl durch Ekins Gesprächseinstieg die Möglichkeit zu einem fachlichen Gespräch bestünde.
Die Szene zeigt prototypisch mögliche Verläufe und Gründe für paralleles Arbeiten. Ein möglicher Grund ist, dass mindestens ein Beteiligter keine Kooperationsbereitschaft signalisiert. Umgekehrt zeigt dies gleichzeitig, dass für eine gemeinsame Fokussierung auf die Aufgabe eine generelle Kooperationsbereitschaft beider Lernender wichtig ist.
Zudem kann diese Interaktionsstruktur emergieren, wenn Lernende durch die gemeinsame Tätigkeit keinen inhaltlichen Gewinn erwarten, z. B. indem ein Lernender die Aufgabe alleine schneller bearbeiten kann oder Lernende nicht davon ausgehen, dass der Mitlernende den Bearbeitungsprozess durch eigene Beiträge aktiv mitgestaltend unterstützen kann.
Die Schülerinnen und Schüler teilen sich arbeitsteilig die Bearbeitung der Aufgabe auf, wobei sie meist nacheinander und abwechselnd tätig werden. Dies bedeutet, dass ein Lernender im Rahmen der intendierten gemeinsamen Tätigkeit alleine die Aufgabe bearbeitet, während der Mitlernende sich inhaltlich nicht beteiligt, sondern die Tätigkeit des Anderen aus einer Beobachterrolle begleitet. Im Regelfall werden im Interaktionsverlauf die Rollen mehrfach gewechselt, sodass beide aktiv an der Aufgabenlösung beteiligt sind. Im Extremfall führt diese Form jedoch dazu, dass ein Lernender die gesamte Aufgabe alleine bearbeitet und die Partnerin oder der Partner am Ende das Arbeitsergebnis übernimmt. Auf diese Weise profitiert sie oder er von der Arbeit des Mitlernenden, ohne einen eigenen, aktiven Beitrag geleistet zu haben. Diese Partizipationsweise lässt sich als „Trittbrettfahrer-Effekt“ (Kerr 1983) beschreiben.
Die Aufgabe wird zwar bearbeitet, allerdings nicht – wie intendiert – innerhalb eines kollektiven Arbeitsprozesses. Punktuell werden mathematische Beiträge geäußert, jedoch nur, um einzelne Fakten mitzuteilen oder um die Bearbeitung der Partnerin oder des Partners zu bestätigen bzw. zu korrigieren, ohne jedoch eigene inhaltliche Lösungsideen zu generieren. Der Schwerpunkt der stattfindenden Gespräche liegt auf sozialen und/oder organisatorischen Themen, wobei vor allem organisatorische Aspekte ausgehandelt werden, um den Arbeitsprozess zu strukturieren und abzustimmen, wer welchen Anteil übernimmt.
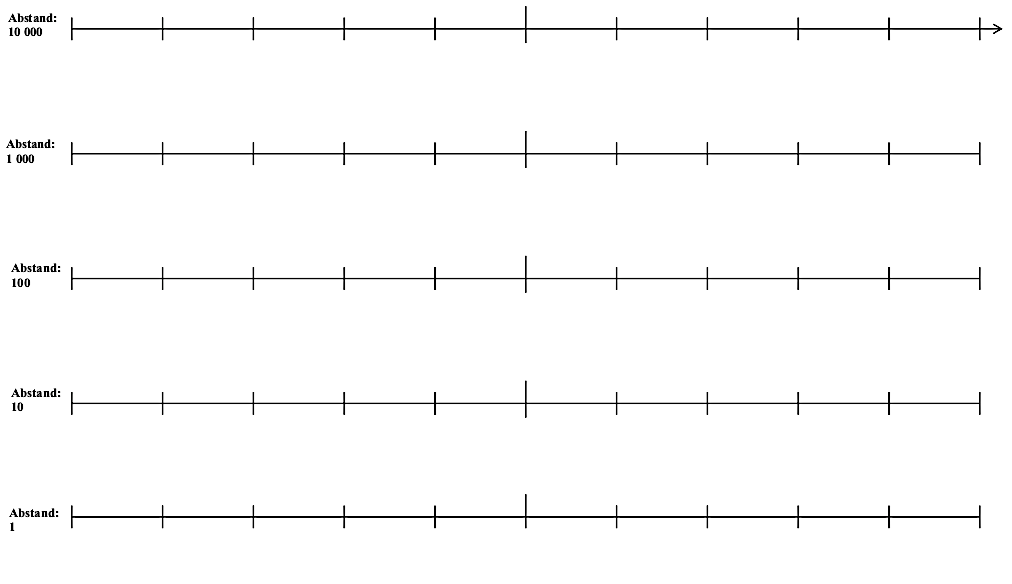
Beispiel: Ayse und Paul sollen gemeinsam fünf Zahlenstrahlen beschriften:

Abb. 2: eingesetzte Zahlenstrahlen
Ayse |
Dann müssen wir die Zahlen reinschreiben. Ich fange an. (notiert auf dem untersten Zahlenstrahl 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40) |
Paul |
Ja, stimmt. Jetzt bin ich dran. Der nächste Zahlenstrahl. (notiert auf dem zweituntersten Zahlenstrahl 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100) |
Ayse |
Ja, das hast du richtig gemacht. Das ist schön leicht die Aufgabe. |
Paul |
Ja, ist sie. Mach jetzt weiter. |
Ayse |
Ja, ich mache ja schon. (notiert auf dem mittleren Zahlenstrahl 0, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000) |
Diese Szene zeigt, dass für beide die Beschriftung der Zahlenstrahlen keine Schwierigkeit darstellt, kein (Er-)Klärungsbedürfnis entsteht und so kein Mehrwert für einen gemeinsamen fachlichen Austausch. Trotz der intendierten gemeinsamen Tätigkeit einigen sich Ayse und Paul stillschweigend die Zahlenstrahlen nacheinander zu beschriften und wechseln regelmäßig die Rollen. Sie bestätigen gegenseitig ihre Lösungen, schätzen die Aufgabenschwierigkeit ein und kommunizieren über organisatorische Aspekte, um den Bearbeitungsprozess und die Rollenwechsel zu steuern. Damit liegt der Fokus nicht auf einer gemeinsamen Aushandlung, sodass auch sie nicht gemeinsam lernen.
Die Interaktion zeigt exemplarisch einen möglichen Grund für ein arbeitsteiliges Vorgehen: In der Situation tritt kein Klärungsbedürfnis auf. Wenn sich Lernende in ihrem Vorgehen oder ihren Lösungen einig sind, werden sie nicht zu einem fachlichen Austausch sowie zu einer Hervorbringung inhaltsbezogener Beiträge angeregt. Daher würde eine fachliche Interaktion den Beteiligten kaum inhaltlichen Gewinn bieten, in der sie gemeinsam mehr erreichen könnten, weshalb die Aufgabe nicht gemeinsam bearbeitet wird.
Prävalente Interaktionen
Prävalente Interaktionen sind durch eine ungleiche individuelle Teilhabe sowie eine unausgewogene Rollenübernahme der Lernenden geprägt. Zwar fokussieren sich beide auf die Aufgabe und es erfolgt ein fachlicher Austausch, in dessen Verlauf Lösungsideen generiert werden sowie beide Lernende wechselseitig aufeinander einwirken. Allerdings übernimmt ein Lernender die Hauptverantwortung für die Hervorbringung der Lösungen, die meistens nicht gemeinsam ausgehandelt werden, organisiert den Arbeitsprozess und koordiniert den Fortgang der Bearbeitung. Damit übt der Lernende einen dominierenden Part aus. Währenddessen äußert der Mitlernende wenige eigenverantwortliche Beiträge und ist daher seltener an der Entwicklung von Lösungsideen beteiligt. Eingebrachte Beiträge der Partnerin bzw. des Partners werden von dem dominanten Lernenden evaluiert, sodass die beiden Lernenden ihre Beiträge nicht gleichberechtigt einbringen können und somit keine Ausgewogenheit in den eingenommenen Rollen entsteht.
In Abhängigkeit von der individuellen Partizipation des dominierten Lernenden lassen sich zwei Arten prävalenter Interaktionen unterscheiden.
Es erfolgt keine gemeinsame Bedeutungsaushandlung im engeren Sinne; vielmehr äußert der dominierende Lernende Lösungen und Ideen, die vom Mitlernenden akzeptiert werden; meistens ohne diese zu hinterfragen. Während der dominierende Lernende sowohl inhaltlich als auch organisatorisch den Interaktionsprozess lenkt, eine unilaterale Kontrolle ausübt sowie teilweise Anweisungen zur Bearbeitung der Aufgabe gibt, bringt die Partnerin oder der Partner wenige inhaltliche Beiträge ein, in denen sich oft eine starke Orientierung an den Handlungen des dominierenden Lernenden rekonstruieren lässt. Aufgrund der ungleichen Rollenübernahme hat der dominierte Lernende wenige Möglichkeiten, aktiv zu partizipieren, sodass die Aufgabenbearbeitung eher einseitig erfolgt.
Beispiel: Jana und Sherin stellen die Zahl 1111 als additive Zerlegung (1000+100+10+1) sowie in der formal-symbolischen Schreibweise dar:
Jana |
Und die Zerlegung? |
Sherin |
Das verstehe ich noch nicht ganz. |
Jana |
Die Zerlegung. Zerlegung ist ja ein Tausender, ein Hunderter, ein Zehner und ein Einer. |
Sherin |
Ja. Also muss ich. |
Jana |
Ein Tausender plus ein Hunderter plus ein Zehner. |
Sherin |
Plus ein Einer? (notiert 1000+100+10+1) So, oder was? |
Jana |
Ja. Und die Zahl. |
Sherin |
Zusammenrechnen? |
Jana |
Hier kommt dann die komplette Zahl hin. Was ist das denn? (..) Erst mal tausend plus hundert. |
Sherin |
Tausend plus hundert? (..) Sind hundert. Neuntausend. Hä? Hunderttausend? |
Jana |
Nein. |
Sherin |
Neuntausend. |
Jana |
Das hier plus das hier. (zeigt auf die 1000 und 100) Das ist ja eine Zahl. (.) Das musst du einfach zusammenrechnen. Eintausend plus hundert. |
Sherin |
Zusammenrechnen. Eintausend plus hundert. (..) Tausendhundert? |
Jana |
Ja. Plus zehn. |
Jana strukturiert den Interaktionsprozess und gibt Sherin Instruktionen, wie sie prozedural vorgehen soll, die ohne Aushandlungsprozess akzeptiert werden. Damit sorgt Jana für ein Vorankommen im Arbeitsprozess. Gleichzeitig orientiert sich Sherin an Jana, obwohl sie den Zahlenraum zuvor bereits erarbeitet hat. In ihren Beiträgen zeigt sich Sherin unsicher, übernimmt Janas Beiträge unhinterfragt und es hat den Eindruck, dass sie viel rät, sodass sie keine eigenverantwortlichen Beiträge äußert und keine gemeinsame Bedeutungsaushandlung erfolgt. Dennoch fokussieren sich beide Schülerinnen auf die zu bearbeitende Aufgabe und es ist eine generelle Kooperationsbereitschaft zu erkennen. Aufgrund fehlender gemeinsamer Aushandlungen und dem Verbleiben auf einer Kalkülebene bieten sich Sherin kaum Chancen, ein Verständnis von der Darstellung natürlicher Zahlen aufzubauen; gleichzeitig scheint Jana auch nicht durch einen reflexiven Blick auf einen vertrauten Zahlenraum profitieren zu können.
Unilateral prävalente Interaktionen sind auch charakteristisch für Interaktion, die gemäß dem Kooperationstyp „Helfen“ (Naujok 2000, S. 176ff) oder „Instruktion“ (Hackbarth 2017, S. 115f) verlaufen. Hierbei gibt der dominierende Lernende Hilfestellungen oder Anweisungen, damit der dominierte Lernende ihre bzw. seine Aufgabe lösen kann und beide fokussieren sich auf die Aufgabe des Hilfeempfängers. Die Partizipation des dominierenden Lernenden lässt sich dann als Hilfegebende und die Partizipation des dominierten Lernenden als Hilfebekommende beschreiben.
Beide Lernende signalisieren die Bereitschaft, sich gemeinsam mit der Aufgabe auseinanderzusetzen, zeigen eine Aufmerksamkeit den Beiträgen des Mitlernenden gegenüber und beteiligen sich aktiv an der Bedeutungsaushandlung. Jedoch werden die Lösungsideen nicht im engeren Sinne gemeinsam ausgehandelt, da aufgrund der unausgewogenen Rollenübernahme beide nicht gleichberechtigt partizipieren. So knüpfen die dominierenden Lernenden meist inhaltlich nicht an die Beiträge des Mitlernenden an, sondern beziehen sich auf ihre eigenen Ideen. Währenddessen greift ihre Partnerin bzw. ihr Partner häufig die Beiträge des dominanten Lernenden auf und versucht diese inhaltlich fortzuführen. Dabei werden die Beiträge im Anschluss von dem dominanten Lernenden evaluiert und entweder bestätigt oder abgelehnt.
Zudem zeigte sich in vielen Interaktionen ein einseitiger Einbezug auf kommunikativer Ebene: Dominierte Lernende sprechen ihre Mitlernenden direkt an, stellen (inhaltliche) Nachfragen und äußern z. T. explizit den Wunsch, dass ihre Beiträge evaluiert werden und sorgen damit für Folgebeiträge des Mitlernenden. Währenddessen bittet der Dominante nicht um eine inhaltliche Einschätzung eines Beitrages und stellt kaum ernstgemeinte Nachfragen.
Beispiel: Aadil und Alex vergleichen Zehntel und Hundertstel nach ihrer Größe:
Alex |
Zehntel sind doch größer als Hundertstel? (..) Weil da, ab da. |
Aadil |
Ja (..) Nein, nein. |
Alex |
Doch. |
Aadil |
Zehntel ist kleiner. Das sind Zehner und das ist Hunderter. |
Alex |
Das muss doch größer sein. Zum Beispiel hattet ihr hier diese, warte mal. (zeichnet einen Kreis) Das hier ist ein Ganzes. Das ist jetzt ein Ganzer. Und jetzt ein Halber. (zeichnet einen neuen Kreis und teilt ihn in zwei gleich große Teile) Was ist größer? Der Ganze oder der Halbe? |
Aadil |
Der Ganze. |
Alex |
Ja. Und wenn man jetzt. Stell dir vor, das sind jetzt Zehner (zeichnet einen Kreis und unterteilt ihn in mehrere gleich große Teile) Stell dir vor, das sind zehn dieser Plättchen. Also nur zehn, das sind genau zehn. Die sind schon recht klein. Und hier (zeichnet einen weiteren Kreis und unterteilt auch diesen in mehrere Teile) wären jetzt hundert dieser kleinen Plättchen. Also viel mehr. Die müssen ja noch kleiner werden, um in so einen Kreis zu passen. Also welche sind größer, die Zehntel oder die Hundertstel? |
Aadil |
Die Zehntel sind größer. Das sind ja nur zehn Plättchen und nicht hundert. |
Alex nimmt einen dominanten Part ein, gibt eine inhaltliche Erklärung, warum Zehntel größer als Hundertstel sind und agiert aus einer Expertenrolle. Trotz des Widerspruchs von Aadil, der zuvor noch nicht mit Dezimalbrüchen gearbeitet hat, setzt Alex seine Idee durch, evaluiert Aadils Beitrag und bezieht Aadil in einer Art Lehrer-Schüler-Gespräch in seine Erklärung ein.
Währenddessen äußert Aadil zwar ebenfalls einen eigenen mathematischen Beitrag, der jedoch von Alex abgelehnt wird, sodass Aadil nicht durch eigenverantwortliche Beiträge an der Generierung der Erklärung partizipiert. Dennoch sorgt Aadil für ein Vorankommen im Interaktionsprozess, indem er durch seine hinreichende Aufmerksamkeit, tätiges Mitdenken und Beantworten der Fragen weitere inhaltsbezogene Beiträge initiiert.
Durch ihre aktive Partizipation scheinen Aadil und Alex inhaltlich profitieren zu können. So erhält Aadil die Möglichkeit, erste verständnisbasierte Einblicke in den Bereich der Dezimalbrüche zu erhalten, während Alex sein Verständnis der Zusammenhänge zwischen gebrochenen Stellenwerten vertiefen kann. Trotz unterschiedlicher Lernvoraussetzungen bietet sich damit beiden Schülern durch die Kooperation Lernpotential auf verschiedenen Ebenen.
Bilaterale Konstruktionen
Beide Lernende sind durch eine aktive und tätige Mitgestaltung an der Bedeutungsaushandlung beteiligt, wobei sich beide auf die Aufgabe fokussieren und Lösungsideen im engeren Sinne gemeinsam entwickeln sowie aushandeln; beide arbeiten also auf ein gemeinsames Ziel hin.
Die individuellen Beiträge werden im Aushandlungsprozess aufeinander abgestimmt und beide können als gleichberechtigte Teilnehmer ihre Gedanken und Ideen einbringen, die gegenseitig aufgegriffen werden. Durch das inhaltliche Anknüpfen (Reziprozität; u. a. Barnes & Todd 1995/2006; Barron 2000; Kumpulainen & Kaartinen 2000) an vorangegangene Beiträge und in dem Zusammenhang zum einen das Aufgreifen von zentralen mathematischen Aspekten der Partnerin oder des Partners sowie zum anderen das Einbringen von etwas Neuem entsteht eine gemeinsame Lösung. Folglich umfassen die Äußerungen eines Einzelnen nicht die gesamte Idee, sondern erst die Beiträge von beiden Beteiligten stellen die gesamte Idee dar (vgl. Barron 2000): „These collaborative actions appear to be formed of chains of utterances in which students weave their joint thinking in turns“ (Kumpulainen & Kaartinen 2000, S. 450). Diese Ausgewogenheit zwischen Aufgreifen und Anknüpfen an bereits Gesagtes sowie das Einbringen neuer Aspekte sorgt für eine wechselseitig beeinflusste Aushandlung und zeigt Akzeptanz sowie Wertschätzung des Mitlernenden. Dies bedeutet nicht, dass beide Lernenden gleich viele eigenverantwortliche Beiträge äußern, sondern dass beide aktiv an der Entstehung der gemeinsamen Lösung beteiligt sind.
Beispiel: Lea und Nele arbeiten alleine an ihren Aufgaben, bevor die individuelle Tätigkeit von Lea unterbrochen wird und sie auf einen Fehler bei Neles Bearbeitung hinweist. In der Aufgabe sollen Zahlen in einer Stellenwerttafel als additive Zerlegung sowie in der formal-symbolischen Schreibweise dargestellt werden.

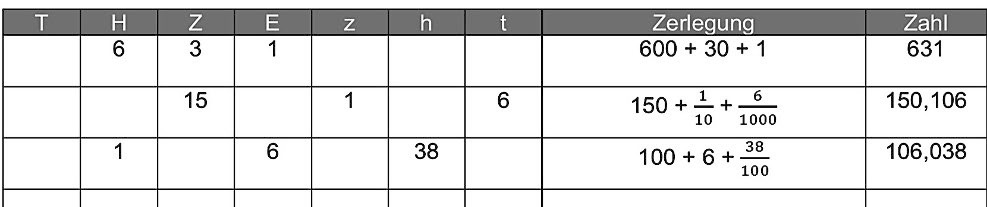
Lea |
Das ist falsch, glaube ich. |
Nele |
Ne, das kann nicht sein. Das ist richtig. |
Lea |
Müsste da nicht die Zahl direkt hinter das Komma? Ich habe hier achtunddreißig Zehner geschrieben. (zeigt auf ihre Stellenwerttafel) Das sind dreihundertachtzig, weil achtunddreißig mal zehn. Und dann geht die drei in Spalte nach links. (zeigt auf die Hunderter-Spalte) Das gilt doch bestimmt auch für deine Zahlen. |
Nele |
Ja, wenn man zehn Zehner zusammenfasst, erhält man einen Hunderter. Da machen dreißig Zehner drei Hunderter. |
Lea |
Ich habe das richtig gemacht, ich weiß. |
Nele |
Und bei mir? (...) Wenn man ein Ganzes in zehn Teile teilt, erhält man Zehntel. Hundertstel sind kleiner als Zehntel. Wenn man zehn Hundertstel zusammennimmt, erhält man nicht Tausendstel, sondern ein Zehntel. Oh, bin ich blöd. Wenn man achtunddreißig Hundertstel hat und zehn Hundertstel einen Zehntel ergeben, dann sind dreißig Hundertstel drei Zehntel. Bleiben noch acht Hundertstel übrig. Dann habe ich drei Zehntel und acht Hundertstel. Das gibt Komma-drei-acht. Stimmt und nicht Komma-null-drei-acht. Danke, Lea. (streicht 106,038 durch und schreibt darunter 106,38) |
Sowohl Lea als auch Nele äußern eigene inhaltsbezogene Beiträge, wobei sie sich jeweils auf Äußerungen der Partnerin beziehen, deren Ideen fortführen und ergänzen (Reziprozität). Dabei lässt sich eine Ausgewogenheit zwischen beiden Schülerinnen erkennen. Obwohl Lea der Bereich der Dezimalbrüche zuvor noch unbekannt war, hinterfragt sie Neles Lösung kritisch und gibt eine Erklärung, warum Neles Ergebnis falsch sein muss. Nele, die zu Beginn noch von der Richtigkeit ihrer Lösung überzeugt zu sein scheint, greift Leas Beitrag auf und berichtigt ihren Fehler. Folglich partizipieren Lea und Nele gleichberechtigt.
Damit zeigt sich exemplarisch, dass gemeinsames Lernen trotz verschiedener Lernvoraussetzungen und Kompetenzen an einem gemeinsamen Gegenstand in inklusiven Lerngruppen möglich ist, wobei die Lernenden gleichberechtigt mathematische Ideen aushandeln und zu gemeinsamen Ergebnissen kommen. Im konkreten Fall scheint Lea die Chance zu haben, erste Einblicke in den Zahlbereich der Dezimalbrüche zu erhalten, während Nele durch einen Rückblick auf natürliche Zahlen ihr Verständnis der dezimalen Stellenwerte vertiefen kann. Damit lernen sie im Sinne eines von- und miteinander Lernens gemeinsam, aber auf verschiedenen Ebenen.
Im Beitrag sollte untersucht werden, welche Interaktionsstrukturen sich innerhalb intendierter Kooperationsphasen an einem gemeinsamen Gegenstand rekonstruieren lassen. Als Ergebnis konnten in einem abduktiven Prozess durch eine Analyse von Schülerinteraktionen und im Vergleich zu vorhandenen Forschungen drei sozial-kommunikative Interaktionsstrukturen herausgearbeitet werden, die sich über (1) die individuelle Partizipation an der gemeinsamen Tätigkeit, (2) die gemeinschaftliche Dynamik der Kooperation sowie (3) die gemeinsame Fokussierung auf die Aufgabe beschreiben lassen. Die Interaktionsstrukturen sind keineswegs trennscharf; die Übergänge sind fließend. Zudem können sich die Interaktionsstrukturen ändern, da die von den Lernenden eingenommenen Rollen und sozialen Beziehungen keinen allgemein validen Zuschreibungen folgen, sondern sich im Interaktionsverlauf dynamisch entwickeln und in den Paaren immer wieder neu ausgehandelt, etabliert oder weiterentwickelt werden.
In dem Zusammenhang zeigte sich, wie Schülerinnen und Schüler mit heterogenen Lernvoraussetzungen auf vielfältige Weise miteinander interagieren und sich am Aushandlungsprozess beteiligen. Durch ihr Einbringen in die Interaktion sind sie aktive „Teilnehmer einer Situation und an deren Definition und Aufrechterhaltung beteiligt“ (Breidenstein 2008, S. 948).
Mithilfe der Interaktionsstrukturen kann das gemeinsame Lernen an einem gemeinsamen Gegenstand im inklusiven Mathematikunterricht erfasst und als empirisches Phänomen beschrieben werden. Dabei befinden sich die Interaktionsstrukturen in einer reflexiven Distanz zu normativen Bedeutungen, da diese Lernsituation didaktisch bereits beschrieben ist (s. o.).
Barnes, D., & Todd, F. (1995/2006). Communication and Learning Revisited. Making meaning through talk. Portsmouth: Heinemann.
Barron, B. (2000). Achieving coordination in collaborative problem-solving groups. Journal of Learning Sciences, 9(4), 403-436.
Beck, C., & Maier, H. (1994). Zu Methoden der Textinterpretation in der empirischen mathematikdidaktischen Forschung. In H. Maier & J. Voigt (Eds.), Verstehen und Verständigung. Arbeiten zur interpretativen Unterrichtsforschung (pp. 43-76). Köln: Aulis.
Boban, I., & Hinz, A. (2003). Index für Inklusion. Lernen und Teilhabe in der Schule der Vielfalt entwickeln. Halle-Wittenberg: Martin-Luther-Universität.
Borsch, F. (2010). Kooperatives Lehren und Lernen im schulischen Unterricht. Stuttgart: Kohlhammer.
Bortz, J., & Döring, N. (2006). Forschungsmethoden und Evaluation für Human- und Sozialwissenschaftler. Heidelberg: Springer.
Breidenstein, G. (2008). Peer-Interaktion und Peer-Kultur. In W. Helsper & J. Böhme (Eds.), Handbuch der Schulforschung (pp. 945-964). Wiesbaden: Verlag für Sozialwissenschaften.
Carle, U. (2017). Eckpunkte für die Entwicklung inklusiven Unterrichts. In F. Hellmich & E. Blumberg (Eds.), Inklusiver Unterricht in der Grundschule (pp. 15-31). Stuttgart: Kohlhammer.
Fetzer, M. (2016). Inklusiver Mathematikunterricht: Ideen für die Grundschule. Baltmannsweiler: Schneider Hohengehren.
Feuser, G. (1989). Allgemeine integrative Pädagogik und entwicklungslogische Didaktik. Behindertenpädagogik, 28(1), 4-48.
Freudenthal, H. (1974). Die Stufen im Lernprozeß und die heterogene Lerngruppe im Hinblick auf die Middenschool. Neue Sammlung, 14(4), 161-172.
Gersten, R., Chard, D., Jayanthi, M., Baker, S., Morphy, O., & Flojo, J. (2009). Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research, 79(3), 1202-1242.
Hackbarth, A. (2017). Inklusionen und Exklusionen in Schülerinteraktionen. Empirische Rekonstruktionen in jahrgangsübergreifenden Lerngruppen an einer Förderschule und an einer inklusiven Grundschule. Bad Heilbrunn: Klinkhardt.
Hähn, K. (2021). Partizipation im inklusiven Mathematikunterricht. Analyse gemeinsamer Lernsituationen in geometrischen Lernumgebungen. Wiesbaden: Springer.
Häsel-Weide, U. (2016). Vom Zählen zum Rechnen. Struktur-fokussierende Deutungen in kooperativen Lernumgebungen. Wiesbaden: Springer.
Häsel-Weide, U. (2017). Inklusiven Mathematikunterricht gestalten. Anforderungen an die Lehrerausbildung. In J. Leuders, T. Leuders, S. Ruwisch & S. Prediger (Eds.), Mit Heterogenität im Mathematikunterricht umgehen lernen – Konzepte und Perspektiven für eine zentrale Anforderung an die Lehrerbildung (pp. 17-28). Wiesbaden: Springer.
Häsel-Weide, U., & Nührenbörger, M. (2015). Aufgabenformate für einen inklusiven Arithmetikunterricht. In A. Peter-Koop, T. Rottmann & M. Lüken (Eds.), Inklusiver Mathematikunterricht in der Grundschule (pp. 58-74). Offenburg: Mildenberger Verlag.
Häsel-Weide, U., & Nührenbörger, M. (2017). Grundzüge des inklusiven Mathematikunterrichts. Mit allen Kindern rechnen. In U. Häsel-Weide & M. Nührenbörger (Eds.), Gemeinsam Mathematik lernen - mit allen Kindern rechnen (pp. 8-21). Frankfurt a. M.: Grundschulverband e.V.
Hengartner, E. (1992). Für ein Recht der Kinder auf eigenes Denken. Die neue Schulpraxis, (7/8), 15-27.
Johnson, D., Johnson, R., & Holubec, E. (2005). Kooperatives Lernen - kooperative Schule: Tipps, Praxishilfen und Konzepte. Mühlheim: Verlag an der Ruhr.
Jungwirth, H. (2003). Interpretative Forschung in der Mathematikdidaktik – ein Überblick über Irrgäste, Teizieher und Standvögel. ZDM, 35(5), 189-200.
Kelle, U., & Kluge, S. (2010). Vom Einzelfall zum Typus. Fallvergleich und Fallkontrastierung in der qualitativen Sozialforschung. Wiesbaden: Springer.
Kerr, N. (1983). Motivation losses in small groups: A social dilemma analysis. Journal of Personality and Social Psychology, 45(4), 819-828.
Korten, L. (2020). Gemeinsame Lernsituationen im inklusiven Mathematikunterricht – Zieldifferentes Lernen am gemeinsamen Lerngegenstand des flexiblen Rechnens in der Grundschule. Wiesbaden: Springer.
Krauthausen, G. (2018). Einführung in die Mathematikdidaktik – Grundschule. Wiesbaden: Springer.
Krauthausen, G., & Scherer, P. (2014). Natürliche Differenzierung im Mathematikunterricht. Konzepte und Praxisbeispiele aus der Grundschule. Seelze: Klett Kallmeyer.
Krummheuer, G., & Brandt, B. (2001). Paraphrase und Traduktion. Partizipationstheoretische Elemente einer Interaktionstheorie des Mathematiklernens in der Grundschule. Weinheim: Beltz.
Kumpulainen, K., & Kaartinen, S. (2000). Situational mechanisms of peer group interaction in collaborative meaning-making: Processes and conditions for learning. European Journal of Psychology of Education, 15(4), 431-454.
Littleton, K., & Häkkinen, P. (1999). Learning Together: Understanding the Processes of Computer-Based Collaborative Learning. In P. Dillenbourg (Ed.), Collaborative Learning. Cognitive and Computational Approaches (pp. 20-30). Oxford: Pergamon.
Lütje-Klose, B., & Miller, S. (2015). Inklusiver Unterricht - Forschungsstand und Desiderata. In A. Peter-Koop, T. Rottmann & M. Lüken (Eds.), Inklusiver Mathematikunterricht in der Grundschule (pp. 10-32). Offenburg: Mildenberger.
Montague, M. (2011). Effective instruction in mathematics for students with learning difficulties. In C. Wyatt-Smith, J. Elkins & S. Gunn (Eds.), Multiple perspectives on difficulties in learning literacy and numeracy (pp. 295-313). Dordrecht: Springer.
Moser Opitz, E. (2014). Inklusive Didaktik im Spannungsfeld von gemeinsamen Lernen und effektiver Förderung. Ein Forschungsüberblick und eine Analyse von didaktischen Konzeptionen für inklusiven Unterricht. Jahrbuch für allgemeine Didaktik, 4(3), 52-68.
Naujok, N. (2000). Schülerkooperation im Rahmen von Wochenplanunterricht. Analyse von Unterrichtsausschnitten aus der Grundschule. Weinheim: Deutscher Studien Verlag.
Nührenbörger, M., & Verboom, L. (2005). Eigenständiges Lernen – Gemeinsames Lernen. Basispapier zum Modul G8 des BLK-Programms "Sinus-Grundschule".
Peter-Koop, A. (2016). Inklusion im Mathematikunterricht. Gemeinsames Lernen am gemeinsamen Gegenstand. grundschulunterricht Mathematik, 63(1), 4-8.
Prengel, A. (2006). Pädagogik der Vielfalt. Verschiedenheit und Gleichberechtigung in Interkultureller, Feministischer und Integrativer Pädagogik. Wiesbaden: Verlag für Sozialwissenschaften.
Scherer, P. (2017). Gemeinsames Lernen oder Einzelförderung? – Grenzen und Möglichkeiten eines inklusiven Mathematikunterrichts. In F. Hellmich & E. Blumberg (Eds.), Inklusiver Unterricht in der Grundschule (pp. 194-212). Stuttgart: Kohlhammer.
Schindler, M. (2017). Inklusiver Mathematikunterricht am gemeinsamen Gegenstand. Mathematik lehren, 201, 6-10.
Schöttler, C., & Häsel-Weide, U. (2017). Students constructing meaning for the decimal system in dyadic discussions: epistemological and interactionist analyses of negotiation processes in an inclusive setting. In J. Novotna & H. Moraova (Eds.), Proceedings of the International Symposium Elementary Maths Teaching. Equity and diversity in elementary mathematics education (pp. 373-383). Prag: Charles University.
Schreiber, C., Schütte, M., & Krummheuer, G. (2015). Qualitative mathematikdidaktische Forschung: Das Wechselspiel zwischen Theorieentwicklung und Adaption von Untersuchungsmethoden. In R. Bruder, L. Hefendehl, B. Schmidt-Thieme & H.-G. Weigand (Eds.), Handbuch der Mathematikdidaktik (pp. 591-612). Heidelberg: Springer.
Steinbring, H., & Nührenbörger, M. (2010). Mathematisches Wissen als Gegenstand von Lehr-/Lerninteraktionen. Eigenständige Schülerinteraktionen in Differenz zu Lehrerinterventionen. In U. Dausendschön-Gay, C. Domke & S. Ohlhus (Eds.), Wissen in (Inter-)Aktion. Verfahren der Wissensgenerierung in unterschiedlichen Praxisfeldern (pp. 161-188). Berlin: De Gruyter.
Transchel, S. (2019). Gemeinsames Lernen multiplikativer Zusammenhänge. Struktur-fokussierende Deutungen bei Kindern mit Schwierigkeiten im Fach Mathematik. Wiesbaden: Springer.
Webb, N. (1989). Peer interaction and learning in small groups. International Journal of Educational Research, 13(1), 21-39.
Winter, H. (2001). Inhalte mathematischen Lernens. Abgerufen von: https://grundschule.bildung-rp.de/fileadmin/user_upload/grundschule.bildung-rp.de/Downloads/Mathemathik/Winter_Inhalte_math_Lernens.pdf [22.01.2021].
Wittmann, E. (1998). Standard Number Representations in the Teaching of Arithmetic. Journal für Mathematik-Didaktik, (2/3), 149-178.
Wocken, H. (1998). Gemeinsame Lernsituationen. Eine Skizze zur Theorie des gemeinsamen Unterrichts. In A. Hildeschmidt & I. Schnell (Eds.), Integrationspädagogik: Auf dem Weg zu einer Schule für alle (pp. 37-52). Weinheim: Juventa.