Thomas Gawlick und Anne Hilgers: Rechenschwäche diagnostizieren und fördern – ein zentraler Baustein des inklusiven Mathematikunterrichts
Abstract:
Thomas Gawlick und Anne Hilgers arbeiten ausgehend von einem Überblick über aktuelle Forschungsansätze und Spannungsfelder der Mathematikdidaktik die besonderen Anforderungen für einen inklusiven Mathematikunterricht heraus. Sie stellen dafür mit dem Bielefelder Konzept zur Diagnose und Förderung bei Rechenschwäche einen wichtigen Baustein vor und erläutern am konkreten Beispiel den Hannoveraner Ansatz zur Vermittlung dieses Konzepts bereits in der ersten Phase der Lehrerausbildung.
Stichworte: Rechenschwäche, inklusiver Mathematikunterricht, Diagnose, Förderung, Seminarkonzept
Inhaltsverzeichnis
- Einleitung
- Anforderungen an die Mathematikdidaktik und daraus resultierende Strömungen
- Aktuelle Entwicklungen der Mathematikdidaktik
- Spannungsfelder und inklusionsspezifische Paradigmen
- Diagnose und Förderung von Rechenschwäche im inklusiven Mathematikunterricht als spezifische Aufgabe der Mathematikdidaktik #
- Literatur
1. Einleitung
Dem Profil des Themenhefts entsprechend, geben wir zunächst einen Überblick über Herausforderungen und Spannungsfelder sowie über aktuelle Entwicklungen der Mathematikdidaktik, wobei wir jeweils bedeutende Protagonisten mit exemplarischen Positionsbestimmungen zu Wort kommen lassen. Dann fokussieren wir auf Diagnose und Förderung im inklusiven Mathematikunterricht als Entwicklungsaufgabe der Mathematikdidaktik. Abschließend stellen wir neben dem Bielefelder Modell zur Diagnose und Förderung von Rechenschwäche auch eigene Ansätze zur Umsetzung durch Forschendes Lernen im Rahmen der Lehrerausbildung vor.
2. Anforderungen an die Mathematikdidaktik und daraus resultierende Strömungen
Um unser Thema im mathematikdidaktischen Diskurs zu verorten, ist eine Positionsbestimmung der Mathematikdidaktik zweckdienlich, denn über ihre Inhalte und Aufgaben gab und gibt es unterschiedliche Auffassungen. Die traditionelle, aber auch heute noch in der Außenperspektive verbreitete Sicht auf die Mathematikdidaktik basiert auf einem rezeptiven Unterrichtsbegriff -Steinbring (1998, 161) bringt das so auf den Punkt: „Parallel zur Deutung des mathematischen Wissens als wohlgeordnetem, fertigem Stoff wird das Unterrichten und Lernen von Mathematik als Stoffvermittlung und Stoffaneignung verstanden.“
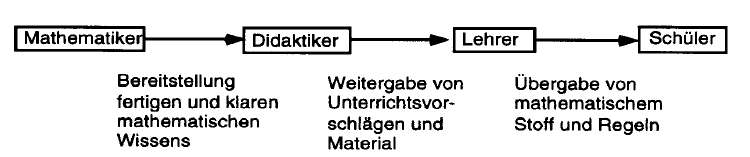
Abb. 1: Rezeptiver Unterrichtsbegriff (Grafik nach Steinbring 1998,165)
Diese traditionelle Sicht (Grafik nach Steinbring 1998,165), gewöhnlich als Stoffdidaktik bezeichnet, gründete sich im Gymnasialbereich auf einer „Elementarmathematik vom höheren Standpunkt“ - so der Titel eines zur Lehrerbildung gedachten Lehrbuchs des einflussreichen Mathematikers Felix Klein. Im Bereich der Volksschullehrerausbildung hingegen fanden im Rahmen einer Methodik des Rechen- und Raumlehreunterrichts (vgl. etwa Karaschewski 1966, Breidenbach 1966) schon immer auch pädagogische und psychologische Aspekte Berücksichtigung, beginnend mit Adolph Diesterwegs didaktischen Impulsen für den Primarunterricht als Leiter eines preußischen Lehrerseminars.
Beim Ausbau des Schul- und Hochschulsektors zur Abwendung der in den 1960er Jahren beschworenen Bildungskatastrophe kam es zu einer Verwissenschaftlichung der Lehrerbildung, in deren Zuge sich die Mathematikdidaktik an den Universitäten etablieren konnte. Im Zuge dessen wurde auch 1975 die Gesellschaft für Didaktik der Mathematik (GDM) gegründet. Neben der traditionellen Stoffdidaktik bildete sich im Laufe der Zeit die qualitativ ausgerichtete Interpretative Unterrichtsforschung heraus, die hervorhob, dass „der Gegenstand mathematikdidaktischer Forschung nicht das mathematische Wissen ‚an sich‘ ist, sondern dass dieses Wissen grundsätzlich im Kontext sozialer Prozesse der Vermittlung verortet werden muss“ (Steinbring 1998,165).
In diesem Kontext wurde erstmals auch das traditionelle Paradigma der fragend-entwickelnden Unterrichtsform als probates Mittel zum Wissensaufbau in Frage gestellt: „In alltäglichen Unterrichtsstunden lassen sich oft Interaktionsmuster rekonstruieren, in denen die Lehrer die Schüleraktivitäten kleinschrittig beeinflussen, ohne dass dadurch günstige Bedingungen dafür geschaffen sind, dass die Schüler wünschenswerte Lernprozesse im Problemlösen und in der Begriffsentwicklung machen.” (Voigt 1994, 82).
Die Interpretative Unterrichtsforschung betrachtet als Gegenstand der Mathematikdidaktik Vermittlungsprozesse mathematischen Wissens in verschiedenen Kontexten – insbesondere im Unterricht. Daraus ergeben sich zweierlei Anforderungen an sie (Steinbring 1998, 165):
- Einerseits konstruktive Anforderungen: Es braucht die Entwicklung von theoretischen Konzepten für innovativen Unterricht und von exemplarischen Lernumgebungen, die nach dem Prinzip des aktiv-entdeckenden und sozialen Lernens zu gestalten sind.
- Andererseits analytische Anforderungen: Die Mathematikdidaktik muss im Wechselspiel mit ihren Bezugsdisziplinen im Sinne einer Ethnographie des Argumentierens (Krummheuer 1995) die Bedingungen, Muster und Strukturen mathematische Diskurse auch im Hinblick auf ihre Besonderheiten analysieren und wissenschaftlich erforschen.
Neben dieser Forschungsrichtung etablierte sich auch eine stärker quantitativ orientierte: Im Zuge des sogenannten PISA-Schocks und der sich anschließenden Umsteuerung in Richtung Kompetenzorientierung (s.u.) kam es zu einer starken Ausweitung der empirischen Bildungsforschung. Diese Akzentverschiebung wirkte (auch materiell) in die Mathematikdidaktik hinein: „ Wo sich Handlungsbedarf in der schulischen Kompetenzförderung abzeichnet, müssen Veränderungsprozesse auf fachdidaktisch-wissenschaftlichen Erkenntnissen aufgebaut und wissenschaftlich begleitet werden, um die Wirkung von Qualitätssicherungsmaßnahmen zu gewährleisten.“ (Reiss & Ufer 2009, 208)
Diese fachdidaktische Forschung im Rahmen der Bildungsforschung ist für eine mangelnde mathematische und mathematikdidaktische Grundierung kritisiert worden (vgl. Keitel & Vithal 2008, 182). Doch sie erhebt für sich den Anspruch, ebenfalls alle Aspekte des Lernens und Lehrens im jeweiligen Unterrichtsfach zu thematisieren (Reiss & Ufer 2009, 200).
Insgesamt dürften die genannten Strömungen sich daher alle mehr oder weniger gut unter der Konzeptualisierung der Mathematikdidaktik als „design science“ wiederfinden, wie sie der einflussreiche Mathematikdidaktiker Erich Chr. Wittmann 1995 einführte und die auch international Anerkennung gefunden hat: „We propose re-conceptualizing the field of mathematics education research as that of a design science akin to engineering and other emerging interdisciplinary fields which involve the interaction of “subjects”, conceptual systems and technology influenced by social constraints and affordances.“ (Lesh & Sriraman, 2005, 490).
Nützlich für das Folgende ist Steinbrings synoptische Darstellung der Dimensionen mathematikdidaktischer Forschungen (s.u. Steinbring 1998, 165), denn diese weist neben der konstruktiven und der analytischen auch bereits eine diagnostische Dimension auf. Auf letztere geht Steinbring in seinem Artikel zwar nicht weiter ein, sie ist aber unter der Inklusionsperspektive bedeutsam.
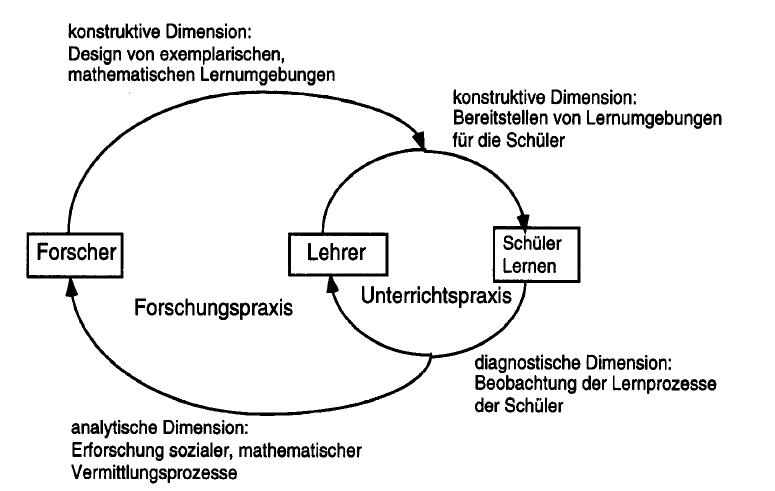
Abb. 2: Dimensionen mathematikdidaktischer Forschungen (Steinbring 1998, 165)
Insgesamt kann man also in der Mathematikdidaktik mehrere auch heute noch einflussreiche Strömungen oder (in chronologischer Sicht) Wellen ausmachen:
- Stoffdidaktik: Fokus auf Unterrichtskonzeptionen
- Interpretative Unterrichtsforschung: Fokus auf der qualitativen Analyse von Lern-Situationen
- Design Science: Fokus auf Entwurf und Beforschung von Lehr-Lern-Arrangements
- Mathematikdidaktik im Rahmen der Bildungswissenschaften: Fokus auf Vergleichsstudien zum Kompetenzerwerb in vorfindlichem Unterricht
Unsere Überlegungen zu Diagnose und Förderung von Rechenschwäche verstehen sich dabei als Beitrag zu einer „design science“ von inklusiven mathematischen Lehr-Lern-Arrangements.
3. Aktuelle Entwicklungen der Mathematikdidaktik
Hier möchten wir im Hinblick auf unsere Zielperspektive nur Folgendes herausgreifen: Die Kompetenzorientierung im Mathematikunterricht und in den ihn begleitenden Abschlussprüfungen und Vergleichsuntersuchungen, sowie, als weiteres diskursbestimmendes Konzept, die Winterschen Grunderfahrungen als Beitrag des Faches Mathematik zur Allgemeinbildung.
3.1 Das diskursbestimmende Konzept der Kompetenzorientierung
Als Folge von internationalen Schulvergleichsstudien wie TIMSS und PISA kam es, wie oben angerissen, zu einer empirischen Wende in den Bildungswissenschaften und den beteiligten Fachdidaktiken sowie in der Bildungspolitik: Bereits die TIMS-Studie zeigte 1995, dass in Deutschland am Ende der Sekundarstufe I in Mathematik „ein bestenfalls mittleres Grundbildungsniveau“ erreicht wurde(Baumert et al., 2000, 163). Dies wurde bemessen an einem länderübergreifenden Kerncurriculum (ebd., 192), bestätigte sich aber auch in der PISA-Studie mit ihrem stärker auf Ermöglichung gesellschaftlicher Teilhabe ausgerichteten Kompetenzbegriff einer „mathematical literacy“ (Baumert et al. 2001).
Aus diesen Ergebnissen zog man den Schluss, von der in Deutschland bis dato praktizierten „Input-Steuerung“ über Lehrplanziele zu einer „Output-Orientierung“ überzugehen, einhergehend mit einem Festlegen und regelmäßigen Überprüfungen der erwarteten Kompetenzen: „Based on these findings, policy makers took measures-programs to improve instructional quality were created, funding of schools was increased, and most importantly, a reform of the education system itself was initiated […] The core of the reform was a growing acceptance of the notion of literacy over the traditional German notion of education.” (Neumann et al. 2010, 546). Der Paradigmenwechsel im Bildungswesen findet seinen Niederschlag in der bildungswissenschaftlichen Expertise zur Entwicklung der nationalen Bildungsstandards (Klieme et al. 2003), die anschließend in den KMK-Standards (KMK 2004) und den Kerncurricula der Länder umgesetzt wurde.
Bei der Standards-Entwicklung berief man sich auch auf das Konzept der heute noch international wirkmächtigen Realistic Mathematics Education (RME), die eine unterrichtliche Sinngebung mathematischer Begriffe aus alltagsweltlichen Bezügen propagiert. Dass mathematische Begriffe zur strukturierten Beschreibung materieller, sozialer und mentaler Phänomene erschaffen wurden und deshalb auch so eingeführt werden sollen (Freudenthal 1983, ix), wird dabei im „framework for assessment“ von PISA (OECD 1999) zur Legitimation des „literacy“-Konzepts herangezogen.
Die veränderte Blickrichtung hin zur Alltagstauglichkeit stieß indes durchaus auf Kritik, insbesondere bei Verfechtern des klassischen deutschen Konzepts einer Allgemeinbildung, wie es von Comenius bis Klafki vertreten wurde. Während die Kritiker die Reduktion auf den Kompetenzbegriff als ein bloß arbeitsmarkttaugliches Rumpfkonzept verurteilten, betonten die Protagonisten den Vorteil einer solcherart eingeengten Konzeptualisierung: „Man kann gar nicht nachdrücklich genug betonen, dass PISA keineswegs beabsichtigt, den Horizont moderner Allgemeinbildung zu vermessen, […] Es ist gerade die Stärke von PISA, sich solchen Allmachtsfantasien zu verweigern und sich stattdessen mit der Lesekompetenz und mathematischen Modellierungsfähigkeit auf Basiskompetenzen zu konzentrieren.“ (Baumert et al 2001, 17) Denn diese Beschränkung auf eine „funktionale Sicht mathematische und naturwissenschaftliche Kompetenzen als basale Kulturwerkzeuge rechtfertigt den Anspruch auf deren Universalisierung.“ (Baumert et al. 2000, 86)
3.2 Ziele eines allgemeinbildenden Mathematikunterrichts
Um die Jahrtausendwende kam es zu einer Diskussion über die Ziele (und damit auch Inhalte und Methoden) des Mathematikunterrichts. Diese speiste sich einerseits aus der angesprochenen Kritik an der Kompetenzorientierung, andererseits aus den Reaktionen auf Hans Werner Heymanns Versuch, auf bildungswissenschaftlicher Grundlage den Bildungsauftrag des Mathematikunterrichts zu bestimmen: Heymann (1996, 50ff) leitete zunächst sieben Aufgaben der allgemeinbildenden Schule her und untersuchte, wie diese mit im Fach Mathematik unterrichtlich zu erfüllen sind:

Abb. 3: Aufgaben der allgemeinbildenden Schule nach Heymann (1996, 50ff)
Eine öffentlich geführte Kontroverse entbrannte darüber, inwieweit diese sieben Aufgaben eine tragfähige Grundlage bilden, um bestimmte (liebgewonnene oder für unverzichtbar gehaltene) Gegenstände des Mathematikunterrichts der Sekundarstufe zu legitimieren: Nachdem der damalige Niedersächsischen Kultusminister Rolf Wernstedt in einer Pressekonferenz auf Heymanns Habilitationsschrift verwiesen hatte, veröffentlichte die dpa eine Agenturmeldung unter dem Titel „Mathematik – in sieben Jahren ist das Wichtigste gelernt“, die von zahlreichen Zeitungen aufgegriffen und noch dabei weiter verknappt wurde („Sieben Jahre Mathematik sind genug“ hieß es etwa in den Ruhr-Nachrichten). Die Kontroverse darüber hätte auch entschärft werden können – denn faktisch formulierte Heymann kein solches Verdikt, sondern eine bedingte Schlussfolgerung: „Erwachsene, die nicht in mathematikintensiven Berufen tätig sind, brauchen für ihren privaten und beruflichen Alltag nur relativ wenig Mathematik - was über den Stoff hinausgeht, der üblicherweise bis Klasse 7 unterrichtet wird (Prozentrechnung, Zinsrechnung, Schlußrechnung), spielt später kaum noch eine Rolle." (Heymann 1996, 214) Zudem reduziert sein Ansatz den schulischen Bildungsauftrag gerade nicht auf eine Lebens- oder gar nur Berufsvorbereitung, sondern stellt ja weitere sechs Aufgaben. Umgekehrt lässt sich aus diesen aber auch kein weitergehender fachinhaltlicher Kanon ableiten - die gesellschaftliche Funktion von Bildung bedingt keinen diesbezüglichen Determinismus, wie etwa Tenorth (2011, 260) hervorhebt.
Im Verlauf der Diskussion brachte der renommierte Mathematikdidaktiker Heinrich Winter als durchaus kritische Gegenposition zu Heymanns (verkürzt interpretierter) Position sein Konzept der mathematischen Allgemeinbildung ins Spiel (Winter 1995, 37):

Abb. 4: Drei Grunderfahrungen im Mathematikunterricht (Winter 1995, 37)
Diese drei Winterschen Grunderfahrungen spannen einen Bogen zwischen der Eigendynamik des Faches, seiner lebenspraktischen Anwendung und persönlichkeitsbildenden Kraft und erfreuen sich weitreichender Zustimmung und vielfacher Anwendung.
Diese Grunderfahrungen dienten den Protagonisten einer kompetenzorientierten Neugestaltung der Curricula als Basis für den Brückenschlag zu ihren Kritikern - rückblickend argumentieren Klieme et al. (2010, 90): Damit bei der funktionalistischen Sichtweise die Eigendynamik der Mathematik nicht zu kurz komme, bezögen sich (die (teils identischen) Autoren der BLK-Expertise (BLK 1997) implizit auf Winters „in gewisser Weise vorbildlich austarierte Bestimmung des Allgemeinbildungsauftrags des Mathematikunterrichts. […] In der mathematikdidaktischen Konkretisierung der welterschließenden Funktion von Mathematik konvergieren Grundbildung und Mathematical Literacy in bemerkenswerter Weise. Auch hinsichtlich der konzeptuellen Integration von fachlichen Kompetenzen, Haltungen und sozialen Fähigkeiten unterscheiden sich Grundbildung und Literacy kaum.“ Hiermit werden also die erste und die dritte Wintersche Grunderfahrung unter das „literacy“-Konzept gefasst und um die zweite ergänzt zur curricularen Konkretisierung des Allgemeinbildungsbegriffs. Dieser ist tragfähig, denn charakteristisch für die Mathematik ist ja gerade das Spannungsverhältnis zwischen erster und zweiter Grunderfahrung, in dem sich die Doppelnatur der Mathematik von Abbildfunktion und systemischem Charakter spiegelt und das von der BLK-Expertise aufgegriffen wird: „Die breite Anwendbarkeit verdankt die Mathematik ihrem abstrakten und formalen Charakter […] Die Dynamik der Mathematik […] wird andererseits erzeugt aus dem freien, kreativen, oft vom Erstaunen ausgehenden, an ästhetischer Darstellung orientierten und den Dialog suchenden intellektuellen Handeln.“ (BLK 1997, 34).
Die drei Grunderfahrungen wurden mehr oder weniger wortgetreu in den Bildungsstandards für Mathematik (KMK 2004) als Beitrag des Faches Mathematik zur Bildung beschrieben (und entsprechend in die Ländercurricula übernommen). Auf dieser Basis werden neben fachspezifischen auch allgemeine mathematische Kompetenzen definiert, die sich in der Visualisierung kranzartig um die ersteren legen, beim Lernen von Mathematik also in diese verwoben sein sollen (KMK 2004,7):
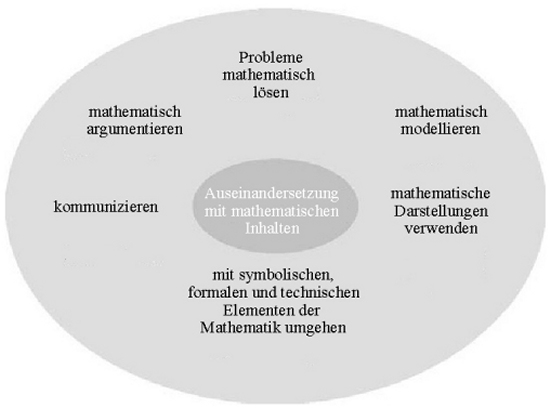
Abb. 5: Allgemeine mathematische Kompetenzen (KMK 2004, 7)
4. Spannungsfelder und inklusionsspezifische Paradigmen
4.1 Mathematikdidaktische Spannungsfelder in Forschung, Lehre und Unterrichtspraxis
Fassen wir das Bisherige zusammen: Aus den unterschiedlich akzentuierten Reaktionen auf die verschiedenartigen Anforderungen an die Mathematikdidaktik heraus haben sich mehrere Strömungen entwickelten, die jeweils ihr Augenmerk verstärkt auf fachliche oder prozessbezogene Aspekte des Unterrichts oder auf den resultierenden Kompetenzerwerb richteten.
Die in Teil 2 skizzierte Fortentwicklung der Mathematikdidaktik über eine bloße Stoffdidaktik hinaus, die einerseits mit detailgenauem Blick auf die interaktive Konstruktion mathematischen Wissens und ihre Kontextbedingungen schaut, und andererseits den Fokus erweitert auf die Erreichung der dabei erforderlichen bzw. erwünschten Kompetenzen in der Breite, wird auch in den in Teil 3 besprochenen Trends deutlich, die über veränderte curriculare Rahmenbedingungen auch Unterrichtspraxis und Lehre umgestalten.
Als aktuelles Spannungsfeld resultiert daraus zunächst das zwischen bloßer Kompetenzorientierung und weitergehendem Bildungsauftrag des Faches: Der Trend zur Kompetenzorientierung und -überprüfung ist dafür kritisiert worden, dem „mählichen Verschwinden des Fachs aus der Mathematikdidaktik“ (Jahnke 2010) Vorschub zu leisten – denn für die Abkehr von der Stoffdidaktik wird ein Schulterschluss von Mathematikdidaktik‘ mit Psychologie und Bildungsforschung (Wittmann 2014, 16) verantwortlich gemacht.
Öffentliche Aufmerksamkeit erfuhr dies in der Debatte darüber, ob in den reformierten Abschlussprüfungen das Niveau sinke – die Kritiker konstatieren: „Die Abituraufgaben entfernen sich immer mehr von der modernen Mathematik als Struktur-Wissenschaft und wenden sich – vielleicht im Sinne einer missverstandenen mathematischen Modellierung – in wortreichen Textaufgaben zahlreichen Anwendungen zu, und das mit wachsendem Einsatz des Taschenrechners […]. Statt mit mathematischen Problemen müssen die Abiturienten mit Formulierungsproblemen kämpfen. […] Letztlich wertet diese Praxis mathematisches Verständnis gegenüber anderen „Kompetenzen“ systematisch ab. Auch an den Aufgaben in Schulbüchern und in Testaufgaben bei PISA wird diese Tendenz sichtbar.“ (Jahnke et al. 2014,120)
Hierfür sehen wir zwei strukturelle Ursachen, die im auch Hinblick auf das Spannungsfeld Inklusion im Blick zu behalten sind: Angesichts der unbefriedigenden Effizienz des althergebrachten mathematisch-naturwissenschaftlichen Unterrichts war es sicher sinnvoll, den Fokus in normativer und deskriptiver Hinsicht stärker der auf die Erreichung der dabei erforderlichen bzw. erwünschten Kompetenzen in der Breite auszuweiten. Eventuell fehlt es durch diese Verbreiterung des Blickwinkels aber auch an Tiefenschärfe, zumal zwecks Umsetzung der politischen Vorgaben in kurzer Zeit neue administrative Strukturen und Forschungsverbünde geschaffen werden mussten.
Dies leitet über zu einem weiteren strukturellen Problem: Man begann mit der Setzung von verbindlichen Standards und dann auch mit der Entwicklung von Verfahren der Standardüberprüfung aber erst deutlich später folgten Überlegungen und Maßnahmen zur Standardumsetzung, insbesondere durch Fortbildung der Lehrpersonen. Diese zeitigt indes nach Einschätzung eines Mitglieds im Vorstand des Deutschen Zentrums für Lehrerbildung Mathematik (DZLM) bislang wenig überzeugende Ergebnisse. (Leuders 2011,288) Als Ursachen machte Leuders dafür einerseits ein Beharren der Lehrerfortbildung auf bewährten Strukturen aus (sicher auch aus administrativen und finanziellen Gründen), anderseits verweist er auf ein Grunddilemma, das Altrichter (2010, 36) so benannte: „Eine Politik, die aus einem Zweifel an der professionellen Selbstentwicklungsfähigkeit der Lehrpersonen und Schulen entstanden ist, appelliert an die Professionalität des schulischen Personals, aus Datenrückmeldung Konsequenzen der Qualitätsentwicklung zu ziehen. […] Wenn die Nutzung von Lernstandserhebungen einen (kompetenzorientierten) ‚Paradigmenwechsel‘ im Lehrerhandeln, wenn sie eine ‚neue Professionalität‘ erfordert, dann setzt das Steuerungsinstrument Datenfeedback gerade das voraus, in dessen Richtung es ‚steuern‘ soll.“
Die oben genannten Wirkfaktoren sehen wir auch bei einem weiteren Spannungsfeld, dem unser Hauptaugenmerk gilt: Der Umsetzung der Inklusion.
Offen bleibt, ob und inwieweit hier ein Umsteuern noch möglich (und gewollt) ist. Im Folgenden beschreiben wir die Rahmenbedingungen für eine nachhaltige Umsetzung der Inklusion im Mathematikunterricht, greifen einen konkreten Beitrag der Mathematikdidaktik dazu genauer auf und machen einen Vorschlag zu seiner Umsetzung.
4.2 Inklusionsspezifische Paradigmen der Mathematikdidaktik
Unter den aktuellen bildungspolitischen Themen nimmt – nicht nur in der Mathematikdidaktik – der Umgang mit Heterogenität derzeit einen hohen Stellenwert ein. Denn hier besteht besonders großer Handlungsbedarf: Bereits Kucharz & Wagner (2007, 156) konstatierten, dass den Lehrkräften gerade im Fach Mathematik fachdidaktische Konzepte für den Umgang mit heterogenen Lerngruppen fehlen. Nachaktuellen Erhebungen von Korff (2015) bei Grundschullehrkräften besteht dieses Manko fort.) Dass der Beitrag der Mathematikdidaktik hierzu noch ausbaufähig ist, konstatieren auch die Herausgeber des Heftes Inklusion der Zeitschrift mathematik lehren: „Wir haben bisher kaum fertig ausgearbeitete oder gar erprobte Konzepte und können nur begrenzt auf Erfahrungen zurückgreifen.“ (vom Hofe & Tiedemann, 2017, 2). Ein solches ausgearbeitetes und erprobtes Konzept beschreiben wir im folgenden Kapitel: Das Bielefelder Förderkonzept bei Rechenstörungen.
Zuvor aber: Was genau bedeutet Inklusion im Mathematikunterricht und was macht sie auf verschiedenen Ebenen des Bildungssystems zur besonderen Herausforderung? Während der Entstehung dieses Artikels wurde hierzu ein Positionspapier der Gemeinsamen Kommission Lehrerbildung der GDM, DMV und MNU veröffentlicht, das zeigt: Der Diskurs steht am Anfang, ist aber bereits sehr vielgestaltig – mit Beiträgen aus der Mathematikdidaktik, der Sonder- und Inklusionspädagogik, aber auch aus psychologischer und medizinisch-therapeutischer Perspektive. Die verschiedenen Disziplinen verwenden dabei jeweils eigene Begrifflichkeiten und folgen unterschiedlichen Handlungs- und Forschungslogiken – und das oftmals, ohne sich wechselseitig zur Kenntnis zu nehmen. Das ist misslich, da im Handlungsfeld Schule Akteure mit recht unterschiedlicher Fachlichkeit aufeinandertreffen. Ein disziplinübergreifender Diskurs wäre daher wünschenswert, um diese mit ihrer domänenspezifischen Expertise einzubinden.
Denn wie im o.a. Positionspapier konstatiert: „Inklusiver Unterricht stellt Lehrkräfte vor viele Herausforderungen, nicht nur in fachdidaktischer Hinsicht, sondern auch in schulpädagogischer (Umgang mit Unterrichtsstörungen, Bedarf an Zusatzbetreuung durch Schulbegleitung etc.), rechtlicher und struktureller (Unsicherheiten und zum Teil unklare Rahmenbedingungen je nach Bundesländern und Schulformen… und vor allem auch personeller Hinsicht (durch systematische Unterausstattung an Betreuungskapazitäten). Da die letztgenannten Herausforderungen nicht durch fachdidaktische Ansätze zu lösen sind, ist in Aus- und Fortbildung nach wie vor eine gewisse Dominanz fachunabhängiger Perspektiven festzustellen.“ (ebd., S.1) Die fachdidaktische Diskussion fokussiert zudem - wie oft auch die Praxis - tendenziell eher auf ein engeres Inklusionsverständnis.
Welche diagnostischen und unterrichtsplanerischen Anforderungen ergeben sich nun konkret, wenn im allgemeinbildenden Mathematikunterricht explizit auch Lernende mit besonderen, insbesondere sonderpädagogischem Unterstützungsbedarf einbezogen werden? Diesbezüglich hat es Natascha Korff im Theorieteil ihrer Dissertation (Korff 2015) unternommen, einige disziplinäre Perspektiven zueinander in Beziehung zu setzen: Ausgehend vom inklusionspädagogischen Forschungsstand zu gutem inklusiven Unterricht (wobei gut bedeutet, dass er Teilhabe und nicht nur Teilnahme am „Bildungsprozess“ ermöglicht) legt sie dar, dass dieser anschlussfähig ist zum fachdidaktischen Diskurs über guten Mathematikunterricht, dem sie zwei weithin geteilte Qualitätsmerkmale eines solchen Unterrichts entnimmt (ebd., 58):
- Aktiv entdeckendes Lernen (aus der Perspektive der „design science“)
- Kognitive Aktivierung (vom bildungswissenschaftlich informiertem Standpunkt)
Davon ausgehend markiert sie zunächst folgende Anknüpfungspunkte für den inklusiven Mathematikunterricht (ebd., 101ff):
1. Beim Lerninhalt: fundamentale Ideen, Anwendungs‐ und Strukturorientierung (dazu vgl. oben die Ziele eines allgemeinbildenden Mathematikunterrichts)
2. Beim Lernprozess: Selbsttätigkeit, individuelle Wege und Kommunikation (als Konsequenz der Analyse empirischer Lehr-Lern-Prozesse, vgl. Abb. 2)
3. Bei der Lernsituation: Herausfordernde Lernanlässe, produktive Übungsformen und verständnisförderliche Arbeitsmittel (anhand der Realisierung des „design science“-Ansatzes)
Um ein solches – auf der Verbindung der Analyse exemplarischer Lernwege mit stoffdidaktischen Konzeptionen fußendes – Rahmenkonzept mit Leben zu füllen, bestehen nach Korff (ebd., S104ff.) folgende Desiderate:
- „ Entwicklung von Hilfen aus, die – auch bei komplexem Unterstützungsbedarf – die selbstständige Entwicklung von Lösungswegen nicht einschränken, sondern unterstützen.“
- „Unterstützung für die Ausbildung elaborierterer Verbalisierungsstrategien“ und „Entwicklung alternativer Kommunikationsmethoden […] mit Bezug auf den Ausdruck von und Austausch über (mathematische) Lösungswegen.“
- „Konzeptionen und Materialien zur entdeckenden Erarbeitung auch basaler Lerninhalte […], die noch über die sog. Vorläuferfähigkeiten hinausgehen.“
Ein gelingender inklusiver Mathematikunterricht findet also die Balance zwischen individuellem und gemeinsamen Lernen (Häsel-Weide & Nührenbörger 2013, Leuders & Prediger 2016): Alle Lernenden, mit und ohne Förderbedarf, sollen gemäß ihrer Lernvoraussetzungen gefördert werden im Sinne einer fachdidaktisch informierten Unterstützung auf individuell stimmigen Lernwegen. Und die ganze Klasse soll immer wieder auch an gemeinsamen Gegenständen arbeiten (Feuser 1998) – auch aus mathematikdidaktischer Sicht: „Zwar kann gemeinsames Lernen in der Sekundarstufe I nicht flächendeckend realisiert werden, wenn die Lernvoraussetzungen mehr als zwei Entwicklungsjahre auseinandergehen. [Dies ist die fachspezifische Hürde für einen inklusiven Mathematikunterricht!] Dennoch lassen sich zumindest immer wieder begrenzte Phasen des gemeinsamen Lernens einplanen, in denen die Lernenden unterschiedliche Lernstufen und Zugangsweisen aktiv aufeinander beziehen, auch wenn sie an unterschiedlichen konkreten Lernzielen arbeiten.“ (Höveler & Prediger 2017). Die Korffschen Desiderate kommen dabei ins Spiel, wenn dazu Lerninhalte für unterschiedliche Anforderungsniveaus, Lernstufen und Zugänge aufbereitet werden.
Den Gedanken eines inklusiven Mathematikunterrichts als ein Lernen im sozialen Miteinander greifen Bikner-Ahsbahs u.a. (2016) auf und konkretisieren ihn durch drei Gestaltungselemente:
- Die Entwicklungslinie einer zentralen fachlichen Idee wird aufgefächert und damit werden verschiedene Zugänge gleichzeitig ermöglicht (zieldifferenziertes Material).
- Eine Mitmachgeschichte bildet den Rahmen für das sozial-fachliche Miteinander.
- Im Unterrichtsverlauf reagieren die Lehrkräfte auf die Beiträge der Lernenden und regen sie durch gezielte emergente Aufgaben (situativ passende Impulse, die an artikulierte Schülervorstellungen anknüpfen)zu individuellen, adäquaten Lernfortschritten an.
Bei solchen Ansätzen inklusiven Unterrichts werden hohe Anforderungen an die diagnostische Kompetenz der Lehrenden gestellt. Es gilt, Inhalte fachlich zu durchdringen, mögliche Lernschwierigkeiten zu antizipieren, Angebote für unterschiedliche Niveaus zu ermöglichen und die verschiedenartigen Denkwege der Lernenden zu erfassen und angemessen aufzugreifen.
5. Diagnose und Förderung von Rechenschwäche im inklusiven Mathematikunterricht als spezifische Aufgabe der Mathematikdidaktik
5.1 Das Phänomen Rechenschwäche – kontroverse Perspektiven
Wie Rechenschwäche konzeptualisiert wird, hängt stark davon ab, auf welchem Hintergrund dies geschieht – und mit welcher Zielrichtung. Die resultierende Befundlage wird in der Expertise „Mathematik entlang der Bildungskette“ (Tenorth et al. 2010 im Auftrag der Telekom-Stiftung) so eingeschätzt: Es „werden lernpsychologische Ansätze zwar intensiv genutzt, aber noch kaum mit fachdidaktischen Forschungen eng verbunden. Neben der je disziplinären Zentrierung der Forschungen zum Kompetenzaufbau dominieren dann eindeutig und im Volumen nahezu monopolartig schulbezogene und dann wieder schulstufenorientierte Arbeiten, meist noch konzentriert auf das allgemeinbildende Schulwesen. Eine Systematik des Kompetenzaufbaus und der Bedingungen der Kompetenzentwicklung ist dabei bisher nicht erarbeitet worden.“ (ebd., 29f) Als „Phänomenbefund“ konstatierte die Expertengruppe, dass die Betroffenen zwar mehr Fehler machen als andere Lernende - aber nicht systematisch unterschiedliche, was die Diagnostik ja sehr vereinfachen würde. Zudem lägen sie durch mangelnde Flexibilität der (v.a. zählenden) Rechenstrategien und durch langsameren Übergang zum Faktenabruf in ihrer Lernentwicklung deutlich zurück. (ebd., 35) Die fachspezifischen Sichtweisen im Einzelnen:
Die medizinisch-therapeutische Sicht
Fachärzte bescheinigen (zur Beantragung einer Eingliederungshilfe für seelisch behinderte Kinder und Jugendliche nach §35a SGBVII) eine Rechenstörung („Dyskalkulie“), die wie folgt definiert ist: „Diese Störung besteht in einer umschriebenen Beeinträchtigung von Rechenfertigkeiten, die nicht allein durch eine allgemeine Intelligenzminderung oder eine unangemessene Beschulung erklärbar ist. Das Defizit betrifft vor allem die Beherrschung grundlegender Rechenfertigkeiten wie Addition, Subtraktion, Multiplikation und Division, weniger die höheren mathematischen Fertigkeiten, die für Algebra, Trigonometrie, Geometrie oder Differential- und Integralrechnungen benötigt werden.“ (WHO 2014) Diagnostiziert wird dies v.a. über eine signifikant unterdurchschnittliche Leistung in einem standardisierten Test. Diese produktorientierte Diagnostik ist indes z.B. zur Ableitung von Förderplänen nur wenig brauchbar (Schipper 2005a), zumal in der zugrundeliegenden neuro- und kognitionspsychologischen Forschung in der Regel nicht das mathematische Lernen selbst, sondern dessen Voraussetzungen untersucht werden (Gaidoschik 2016).
Die Sicht der Kultusbürokratie
Der niedersächsische Erlass zur Förderung von Schülerinnen und Schülern mit besonderen Schwierigkeiten im Lesen, Rechtschreiben oder Rechnen (vom 04.10.2005) konstatiert besonderen Förderbedarf bei Schülerinnen und Schülern
- „in den Schuljahrgängen 1 und 2, denen die grundlegenden Voraussetzungen für (…) den Erwerb der Grundrechenarten noch fehlen;
- in den Schuljahrgängen 3 und 4, deren Leistungen im (…) Rechnen über einen Zeitraum von mindestens drei Monaten den Anforderungen nicht entsprechen;
- in den Schuljahrgängen 5 bis 10, wenn in Einzelfällen besondere Schwierigkeiten im Rechnen bisher nicht behoben werden konnten.“
Dies ist in der Erlasslage zunächst einmal (losgelöst vom sonderpädagogischen Unterstützungsbedarf) Voraussetzung für zieldifferenten Unterricht. Offen bleibt dabei worin die angesprochenen grundlegenden Voraussetzungen bestehen, wie ihr Fehlen diagnostiziert und auf welche Weise es überwunden werden kann.
Die Sicht der Mathematikdidaktik
Im Gegensatz zu den vorherigen „Diskrepanzdefinitionen“ wird in der Fachdidaktik eine „phänomenologische Definition“ bevorzugt. D.h. man versucht, Phänomene zu beschreiben, die bei rechenschwachen Kindern zu beobachten (und für diese charakteristisch) sind. Wir folgen hierbei Wilhelm Schippers etwas uneinheitlicher Terminologie: Unter besonderen Schwierigkeiten beim Mathematiklernen leiden Kinder, die „den Anschluss an das Klassenniveau verloren haben und ihn ohne qualifizierte Hilfe auch nicht mehr finden.“ (Schipper, 2009, 239) Dagegen spricht Schipper (2005a, 24) unter Verweis auf Lorenz und Radatz (1993, 16) von Rechenschwäche, wenn unabhängig von der Dauer und der Schwere der Beeinträchtigung über den Normalunterricht hinaus weitere (schulische) Fördermaßnahmen benötigt werden und konstatiert: „Im Sinne dieser Definition ist etwa 20% aller Kinder eines Jahrgangs eine Rechenschwäche zuzuschreiben. Es ist wohl selbstverständlich, dass es bei diesen Kindern keinen Grund gibt, außerschulische Einrichtungen mit einer Therapie im Sinne des § 35a zu beauftragen; für die Förderung leistungsschwacher Kinder in Mathematik ist die Schule zuständig.“ (ebd.) Er differenziert: „Eine Rechenstörung ist eine extreme, besonders schwerwiegende und dauerhafte Rechenschwäche […] Ungefähr vier bis sechs Prozent aller Kinder sind hiervon betroffen, was im Durchschnitt einem Kind pro Grundschulklasse entspricht.“ (Schipper, 2009, 332) Rechenschwäche ist also in dieser Sicht genau das, was Förderbedarf verursacht! Inhaltlich gefüllt wird diese Definition freilich erst durch die Identifikation von Symptomen. Den Rahmen dafür stecken Schipper et al. (2011, 12) so ab: „Eine Rechenschwäche kann daher als eine Entwicklungsverzögerung beim Erlernen des Rechnens interpretiert werden, die durch besondere Klippen im mathematischen Lernprozess ausgelöst wird. Die Art der Klippen und Auffälligkeiten bezeichnen wir als Symptome für Rechenstörungen.“
Das Konzept „Rechenschwäche als Entwicklungsverzögerung“ halten wir für inhalts-, stufen- und schulformübergreifend tragfähig und legen es daher im Folgenden zu Grunde. Dabei sind wir uns bewusst, dass das Konstrukt „Rechenschwäche“ durchaus auch von Fachdidaktikern als „unbrauchbar“ abgelehnt wird: So etwa Gaidoschik (2016) unter Verweis auf Meyerhöfer (2011), der vorschlägt, das Phänomen nicht als Rechenschwäche zu konzeptualisieren, sondern als nicht bearbeitete stoffliche Hürden - aus dieser Sicht entsteht die Entwicklungsverzögerung also dadurch, dass die Lernenden beim Überwinden der Klippen nur unzureichend unterstützt werden. Ein Indiz dafür ist das empirische Resultat, dass ein Grundschulunterricht, der verstärkt auf die Vermittlung von Rechenstrategien setzt, das Loslösen vom zählenden Rechnen bei deutlich mehr Kindern gelingt als in einem klassischen Unterricht (Gaidoschik, Deweis & Guggenbichler 2017). Wir verwenden hier und in den unten beschrieben Veranstaltungen dennoch den Begriff Rechenschwäche, um das Gespräch mit den Nachbardisziplinen und der Praxis zu erleichtern.
5.2 Phänomenbasierte Diagnose von Rechenschwäche
Aus den kontroversen Sichtweisen ergeben sich auch abweichende diagnostische Verfahren – wir plädieren mit Schippers Maxime vor: „Diagnostizieren, um zu fördern“ für eine prozess- (und nicht produkt-)orientierte Diagnostik. Dabei ist die vielfältige Phänomenologie der Rechenschwäche konzeptionell zu fassen durch Identifikation bestimmter markanter Verhaltensweisen als Indikatoren für und deren Gruppierung und Deutung als Symptome von Rechenschwäche. Hierfür hat insbesondere Schipper in diversen Publikationen inhaltlich nah verwandte, aber in wichtigen Einzelheiten auch unterschiedliche Vorschläge gemacht. Wir folgen hier Schipper et al. (2011, 15ff.):
- Verfestigtes zählendes Rechnen
- Einschränkungen in Stellenwertverständnis & unzureichende Orientierung im Zahlenraum
- Unzureichende Grundvorstellungen & unzureichende Größenvorstellungen
Gegenüber früheren Vorschlägen (etwa in Schipper 2008, 20ff) wird die Symptomatik nun stärker mittels mathematikdidaktischer Grundideen hin charakterisiert: Das eher fachunspezifische Symptom „Probleme bei der Links-/Rechts-Unterscheidung“ entfiel, an die Stelle „einseitiger Vorstellungen“ treten unzureichende Grundvorstellungen (als deren Zeichen die früher genannten „Intermodalitätsprobleme“ gesehen werden können).
Im Kontext der Entwicklung der Diagnose-Software BIRTE 2 haben Schipper et al. (2011) diese Symptome detailliert durch eine Vielzahl gut operationalisierter Indikatoren für die Symptome sowohl von Rechenschwäche als auch von Rechenfertigkeit beschrieben. Hier zum Überblick darüber ein Strukturbild, das die von uns daraus entnommen Indikatoren den Symptomen zuordnet (mehr dazu s.u.):

Abb. 6: Strukturdiagramm zur Rechenschwäche
5.3 Das Bielefelder Förderkonzept bei Rechenstörungen
Wie bei der Konzeptualisierung und Diagnostik von Rechenschwäche gibt es für die Förderung sehr unterschiedliche Ansätze. Das Bielefelder Konzept basiert auf den obigen konzeptionellen und diagnostischen Erwägungen – diese wurden von Schipper und Mitarbeitern um das in der Bielefelder Beratungsstelle entwickelte Förderkonzept ergänzt und in diversen Publikationen, Lehrerfortbildungen und Theorie- und Förderseminaren vermittelt.
Das Förderkonzept „verfolgt das Ziel, Grundvorstellungen aufzubauen, was durch die Verinnerlichung von Handlungen am Material unterstützt werden soll.“ (Lesemann 2014, 727) denn: „Eine effektive Planung von Diagnose und Fördersituationen kann durch die Orientierung an Grundvorstellungen geschehen.“ (Wartha/Schulz 2012, 41) Hierzu haben Wartha und Schulz anknüpfend an Aebli ein Vier- Phasen-Modell der schrittweise Ablösung vom Material weg vom konkreten Handeln, hin zum „Aufbau entsprechender (visueller) Repräsentationen bzw. Verinnerlichungen, die operatives Handeln auf der Vorstellungsebene (im Sinne Piagets) ermöglichen“ (vom Hofe 1995, 97f.) ausgearbeitet:

Abb. 7: Vierphasenmodell (verändert nach Wartha/Schulz 2012, 63)
Hier ein kurzer Einblick in die entsprechend dazu vorgeschlagenen konkreten Förderaktivitäten:

Abb. 8: Beispiele aus der Bielefelder Förderkartei (Schipper 2005b, 19)
Die Bilder zeigen einerseits, dass der Rechenrahmen im Bielefelder Konzept das zentrale Material zur Ablösung vom Zählenden Rechnen ist. Andererseits wird deutlich, wie Förderer durch die Aufforderung, eine Rechnung an Material zu erläutern, Aufschluss darüber erhalten, ob zu den Rechenwegen auch Grundvorstellungen entwickelt oder ob nur unverstandene Rezepte angewandt wurden. Hier beispielhaft der Grundvorstellungsumweg bei der Aufgabe 7+8:

Abb. 9: Grundvorstellungsumweg (Wartha/Schulz 2011, 6)
Auf entsprechende Weise wird in der Förderung an den weiteren Symptomen gearbeitet – auch hierzu Schlaglichter: Unten sieht man Schritte, derer es bedarf, um ein zureichendes Stellenwertverständnis aufzubauen: Zunächst die Unterscheidung von „Acht“ und „Vierzig“ und dann das Verständnis, dass „Vierzig“ sich als „vier Reihen von zehn Einern“ auffassen lassen. Das schafft einerseits die Verstehensgrundlage für das Bündelungsprinzip und schlägt andererseits eine Brücke zum Operationsverständnis insbesondere der Multiplikation: Im zweiten Bild sieht man, wie die Zehnerbündelung für eine enaktive Darstellung von 5×13 genutzt und in der ikonischen Darstellung weiter schematisiert wird, so dass ein verständiger Übergang zum Normalverfahren ermöglicht wird, das so mit Grundvorstellungen unterlegt wird.

Abb. 10: Übergang von der enaktiven zur symbolischen Darstellung (Rasch 2016, 32)
Der Übergang zu solchen Vorstellungsbildern ist auch vonnöten, da ein bloßes materialbasiertes Arbeiten schnell an Grenzen stößt: Bei der Übertragung der zentralen Strategie „Schrittweise über den Zehner rechnen“ vom Zwanziger- in den Hunderterraum ist der Rechenrahmen das probate Mittel – aber bei Aufgaben des Typs ZE+E sind auch seine Grenzen erreicht: Aufgaben des Typs ZE+ZE lassen sich nicht mehr gut am Rechenrahmen behandeln.

Abb. 11: Zusammenhang zwischen Zahlwort, Zahlzeichen und Menge bei der Entwicklung des Stellenwertverständnisses (Wartha & Schulz 2011, 10)
Für Aufgaben des Typs ZE+Z ist zwar noch der Wechsel zum Dienes-Material denkbar (und zum Verstehensaufbau hilfreich), aber für den Typ ZE+ZE ist auch dieses zu starr. Daher ist die Verinnerlichung unabdingbar – hier gezeigt am Beispiel der Strategie „Schrittweise über den Zehner rechnen“ bei 37+8:


Abb. 12: Beispiele aus der Bielefelder Förderkartei (Schipper 2005b, Karte 13 und 14)
5.4 Ein Seminarkonzept zu Diagnose und Förderung von Rechenschwäche (DuF)
Problemstellung
In Niedersachsen ist die inklusive Schule verbindlich zum Schuljahresbeginn 2013/14 eingeführt worden. Dies stellt insbesondere auch die Förderschullehrkräfte vor neue Aufgaben, die in der Lehrerausbildung angemessen zu berücksichtigen sind. Zu den Aufgaben der zukünftigen SonderpädagogInnen zählen vermehrt:
- Diagnose des Förderbedarfs von SchülerInnen mit besonderen Schwierigkeiten im Rechnen
- Erstellung von Förderplänen
- Durchführen von Förderungen
- Reflektieren von Förderungen
- Beratung von Lehrkräften und Erziehungsberechtigten bezüglich der geeigneten Förderung
Um diese Aufgaben adäquat erfüllen zu können, bedarf es umfangreicher theoretischer und praktischer Erfahrungen zu Rechenschwäche und ihrer Diagnose sowie der Planung, Durchführung und Reflexion von Förderungen. Für das Zweitfach Mathematik für Sonderpädagogen konzipierten wir basierend auf dem Bielefelder Ansatz mathematikdidaktische Veranstaltungen zu Diagnose und Förderung bei Rechenschwäche (DuF), um im universitären Rahmen eine zugleich praxisbezogene und wissenschaftlich fundierte Auseinandersetzung damit zu ermöglichen. Die dabei erreichten Kompetenzen in Diagnose, Planung, Durchführung und Reflexion lassen sich dann auch für andere organisatorische Modelle und inhaltliche Kontexte von Förderung nutzen.
Begründung des Vorgehens
Aus professionstheoretischer Sicht besteht die Aufgabe von Praxisphasen in der Aufdeckung der Differenz von Theorie und Praxis sowie in der Erprobung einer Haltung forschenden Lernens (Blömeke 2001, 137), die durch die Methode der Fallarbeit gefördert wird (ebd. 154). Im Kontext des Hannoveraner Qualitätsoffensive-Projekts „Theoria cum praxi. Förderung von Reflektierter Handlungsfähigkeit als Leibniz-Prinzip der Lehrerbildung“ im Sinne einer Theorieaneignung durch Verstehen von und Anwenden auf Praxis (vgl. Gillen 2015) werden dazu im DuF-Modul videographierte Diagnose- und Fördersituationen zum Ausgangspunkt des Lernens gemacht. Diesem Konzept zur Theorie-Praxis-Verknüpfung liegt die Annahme zugrunde, dass nicht die bloße studentische Praxis-Aktivität, wohl aber die rekonstruktiv-reflexive Auseinandersetzung mit ihr auf dem Hintergrund von fachdidaktischen und bildungswissenschaftlichen Theorienbeständen entscheidend für den Professionalisierungseffekt der Maßnahme ist. Denn aufgrund der Fallstrukturgesetzlichkeit professionellen Handelns bedarf es nach Blömeke (2001,133) der Annahme eines wissenschaftlichen und eines praktisch-pädagogischen Habitus, die im Zuge der Professionalisierung zu verknüpfen sind. Die intendierte Förderung Reflektierter Handlungsfähigkeit im Projekt „Leibniz-Prinzip“ soll sich so vollziehen:
 Abb. 13: Das Leibnizprinzip in der Lehrerbildung (Gillen 2015)
Abb. 13: Das Leibnizprinzip in der Lehrerbildung (Gillen 2015)
Das DuF-Modul zielt dabei auf die Herstellung dieser Verknüpfung im Zuge der Entwicklung fachdidaktischer Teilkompetenzen: Dazu wird zunächst eine „situationssensible Wahrnehmungsfähigkeit“ entwickelt, die dann begründete Handlungsentscheidungen ermöglicht (reflection in action). Diese sind aufgrund der berufsimmanenten Handlungsunsicherheit im Nachgang noch einmal auf ihre Angemessenheit zu prüfen (reflection on action).
Ausgestaltung des Seminarkonzepts
Zur Realisierung der intendierten Theorie-Praxis-Verknüpfung wurde ein Modellprojekt aus Studienqualitätsmitteln beantragt, um den Studierenden eine individuell betreute und anschließend gemeinsam reflektierte Einzelförderung anbieten zu können. Der Lehrgang im Bereich „Diagnose und Förderung bei Rechenschwäche“ erfolgt daher in drei Phasen:
- Seminar „Diagnose und Förderung bei Rechenschwäche planen“ (DuFp) im WS
- Betreute Förderung „Diagnose und Förderung bei Rechenschwäche qualifiziert durchführen“ (DuFq) im Anschluss an das Fachpraktikum in der vorlesungsfreien Zeit
- „Diagnose und Förderung bei Rechenschwäche reflektieren“ (DuFr) im SS
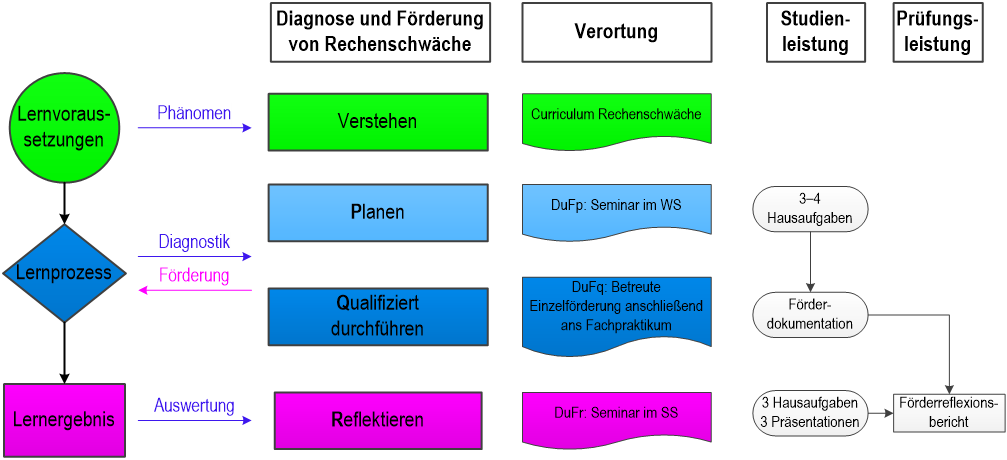
Abb. 14: Seminarstruktur

Abb. 15: Auf dem Weg zur reflektierten Handlungsfähigkeit
Parallelisierte Darstellung der Diagnose von Fördervoraussetzungen und -ergebnissen
Um später die Reflexion durchgeführter Fördermaßnahmen zu erleichtern, haben wir das obige Strukturbild zum Bielefelder Konzept von Rechenschwäche erstellt und um ein gleichartiges zur Rechenfertigkeit ergänzt. Durch eine Parallelisierung der Indikatoren wird der Vergleich erleichtert und besser strukturiert, spezifische Bereiche der Stagnation und des Fortschritts werden besser erkenn- und unterscheidbar. Hier eine Prinzipdarstellung des intendierten Verlaufs – naturgemäß werden bei einem Kind zu Beginn nicht alle Felder rot und am Ende nicht alle Felder grün sein. Das Phänomen Rechenfertigkeit konzeptualisieren wir durch folgende Symptome:
- Strategisches Rechnen (i.e. mittels heuristischer und operativer Strategien)
- Stellenwertverständnis & Orientierung im Zahlenraum angemessen
- Adäquate Grundvorstellungen & Größenvorstellungen
Hierzu stellen wir den Studierenden die folgende, aus Schipper et al. (2011) extrahierte Liste von Indikatoren zusammen:

Abb. 16: Zusammenstellung von Indikatoren für Rechenfertigkeiten (extrahiert aus Schipper 2011)
Anknüpfend an diese Liste können die Studierende anhand des Handbuchs bzw. des Diagnoseleitfadens in Wartha & Schulz (2012) selbständig passende Indikatoren für die Symptome der Rechenschwäche erstellen, indem sie das Verhalten beschreiben, das anstelle des jeweils gewünschten gezeigt wird.
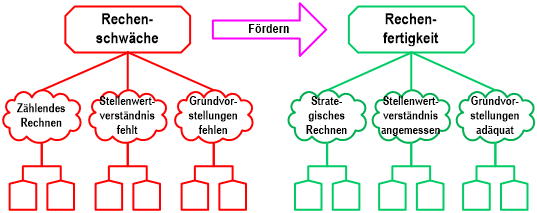
Abb. 17: Der Förderprozess kann mit Strukturdiagrammen genauer beschrieben werden
Der Ablauf von „Diagnose und Förderung von Rechenschwäche qualifiziert durchführen“ (DuFq)
- Durchführung einer Eingangsdiagnostik mit mehreren Kindern (vor oder zu Beginn des Fachpraktikums)
- Begründete Auswahl eines Kindes für die Förderung
- Festlegung von Förderzielen
- Erstellen eines Förderplans
- Durchführung von (mindestens) 8 Förderstunden mit diesem Schüler
- Vor- und Nachbereitung jeder Förderstunde
- Nach der zweiten Förderstunde: Erstellen eines Förderplans für den Schüler
- Durchführung einer Abschlussdiagnostik mit dem zuvor geförderten Schüler
Während der Förderung werden die Studierenden wöchentlich betreut. Dabei werden der Förderplan, die Stundenvor- und -nachbereitungen sowie eine „interessante Stelle“ aus der letzten Förderung besprochen. Sowohl die Diagnostik als auch die Förderstunden sollen von den Studierenden dokumentiert und videographisch aufgezeichnet werden.
Zur Dokumentation gehören:
- schriftliche Vor- und Nachbereitungen jeder Förderstunde
- Videographie und Fotos/Bilder
- Kopie der Eigenproduktionen des Schülers (z.B. bearbeitete Aufgaben, Notizen, etc.)
- Ansatz zur Analyse einer „interessanten“ Stelle im Video (für den Förderreflexionsbericht als PL in DuFr)
- Begründung des Interesses an dieser Stelle
- Beschreibung dieser Stelle unter Heranziehen einer geeigneten Fragestellung
- Mögliche Ansätze zum Beantworten dieser Frage
- Ergebnis der Besprechung mit den Betreuern
- Geeignete Dokumentation des Förderergebnisses: z.B. Retest, Selbst- und Fremdberichte aus dem Unterricht.
Der Ablauf von „Diagnose und Förderung von Rechenschwäche reflektieren“ (DuFr)
Hier werden sowohl die Planung als auch die Durchführung der individuellen Förderung im Lichte der Ein- und Ausgangsdiagnostik einer Reflexion unterzogen. Dabei sollen soweit möglich und sinnvoll auch Methoden der qualitativen (Kategorienbildung) und quantitativen (Häufigkeitsvergleiche) Inhaltsanalyse verwendet werden.
Insbesondere die qualitative Inhaltsanalyse (Mayring 2008) dient hier zum Brückenschlag vom wissenschaftlichen zum praktisch-pädagogischen Habitus: Die Indikatoren in Schipper et al (2011) und Wartha & Schulz (2012) sind als situativ nutzbare Entscheidungskriterien für pädagogisches Handeln formuliert, das sich nach van Manen (1995, 68) „auf dem Niveau des Augenaufschlags“ vollzieht. In der postaktionalen Reflexion dagegen ist es möglich und sinnvoll, den Weg von der Beobachtung über ihre indikatorbasierte Deutung hin zur beurteilenden Schlussfolgerung detailliert nachzuzeichnen. Die Inhaltsanalyse bietet für den ersten Schritt regelgeleitete und theoriebasierte systematische Verfahren, ist also intersubjektiv nachprüfbar und erfüllt sozialwissenschaftlichen Methodenstandards (Mayring 2008, 12): Einschlägig ist hier die typisierende Inhaltsanalyse: dazu werden aus der Theorie Typen ableitet (hier: die Symptome von Rechenschwäche) und durch Kombinationen von Merkmalsausprägungen beschrieben. Die Merkmalsausprägungen (hier: Indikatoren) bilden die Kategorien der Analyse. Anhand eines Teils des Materials (hier: transkribierte Förderungen) wird die Vergabe mittels Kodierregeln und Ankerbeispielen festgelegt (hier: durch Elaboration am Beispiel, wann ein Indikator vergeben wird). Anschließend wird der zur Analyse ausgewählte Teil des Materials kodiert. Dann ist fallbasiert zu klären, welche der gefundenen Indikatorkombinationen Symptome von Rechenschwäche stichhaltig belegen. Das ermöglicht dann, im zweiten Schritt den Förderverlauf zu beurteilen, wie im nächsten Abschnitt gezeigt wird.
Die Ergebnisse werden denen aus der zuvor erschlossenen Literatur gegenübergestellt. Die Videos, die bei Bedarf ausschnittsweise transkribiert werden, dienen als Basis einer Reflexion mit differenziertem Analysefokus sowie zur Generierung und Prüfung von Arbeitshypothesen zum Förderverlauf und zu seinen Einflussfaktoren. Im Folgenden ein Beispiel für drei Analyseebenen, die im Kontext unterschiedlicher Fragestellungen über die Fördersituation ( „Wie heißt die Zahl hinter dem Plättchen?“) gelegt werden:

Abb. 18: Die Videos der eigenen Förderung dienen den Studierenden als Grundlage für eine reflektierte Analyse
5.5 Das Praxisbeispiel Annika
Beispiele aus der Reflexion der Förderung von Annika sollen zeigen, wie im Hannoveraner Projekt konkret gearbeitet wird. Dazu stehen die BIRTE-Ergebnisse (vorher, nachher), Video und schriftliche Auswertung der Erstüberprüfung, Förderbericht, schriftliche Vor- und Nachbereitungen der Förderer und die Fördervideos auf einer E-Learning-Plattform zur Verfügung, die im Rahmen der Maßnahme „Virtuelle Hospitation – Lehr-Lernsituationen multimedial erfahren und erproben“ des Hannoveraner Qualitätsoffensive-Projekts (vgl. Gillen 2015) entwickelt wird.
Die dabei durchlaufenen Schritte sollen die Studierenden dann in der Reflexion ihrer eigenen Förderung entsprechend durchführen.
Schritt 1 der Reflexion: Auswahl des Kindes, Diagnose und Förderziele
Vertiefend zum Bericht können die Studierenden hierbei auch das Video der Erstüberprüfung analysieren - aus Zeitgründen allerdings nur ausschnittsweise. Dies ist dennoch in Annikas Fall sehr aufschlussreich, wie schon die folgenden Strukturbilder der zu den ersten beiden Teilen des Videos passenden Indikatoren für Symptome von Rechenschwäche bzw. -fertigkeit zeigen.

Abb. 19a: Beispielhafte Aufgabenstellung aus dem Seminar DuFp

Abb. 19b: Beispielhafte Bearbeitung aus dem Seminar DuFp
(ZR = Zahlenraum, RR = Rechenrahmen, MSB = Mehrsystemblöcke)

Abb. 20a: Analyse der Erstüberprüfung von Annika (Auszug), Blick auf Rechenfertigkeiten (Auszug)
(RR = Rechenrahmen, MSB = Mehrsystemblöcke)
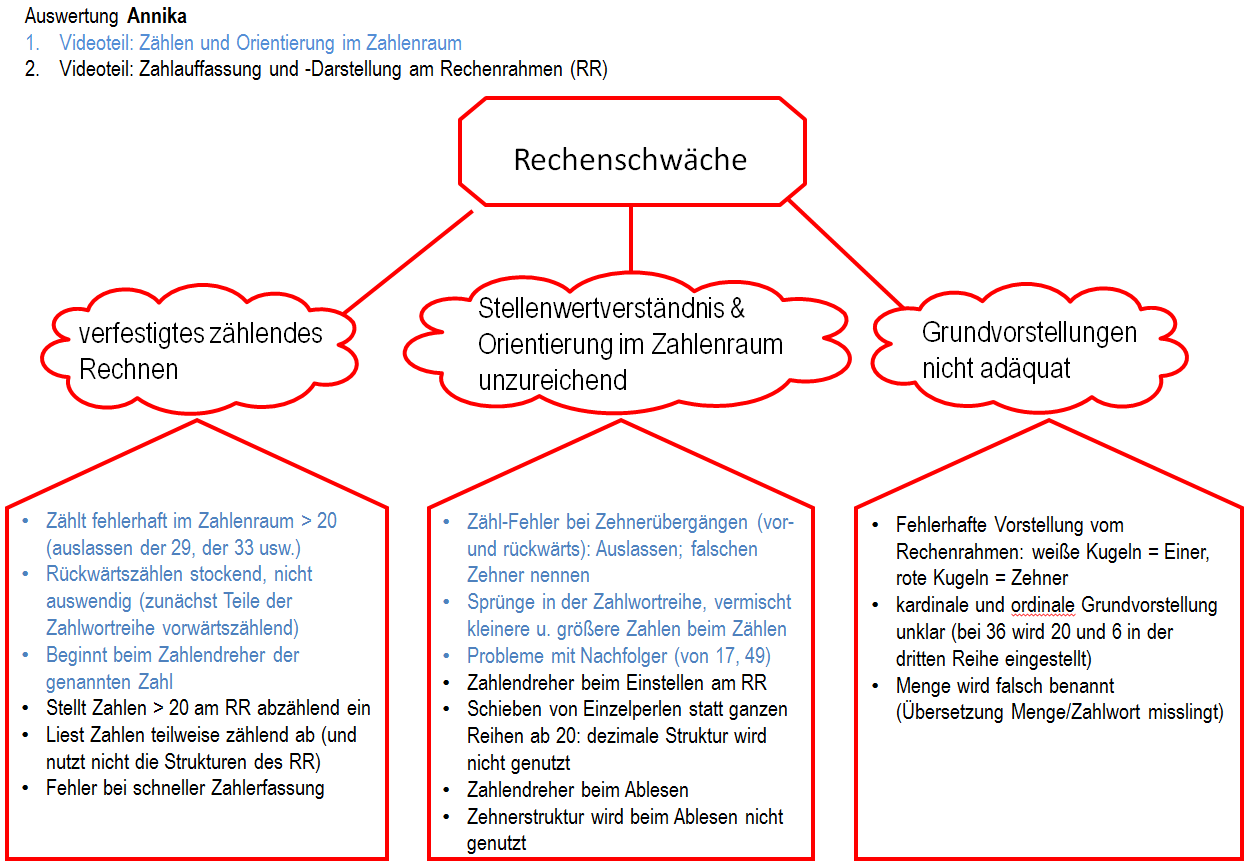
Abb. 20b: Analyse der Erstüberprüfung von Annika (Auszug), Blick auf Rechenschwäche (Auszug)
Die Analyse der Diagnoseergebnisse kann zur Antizipation der Förderplanung dienen, wie folgende Antwortskizze für die Aufgabe e) zeigt. Im nächsten Schritt kann diese dann genutzt werden, um die Planung der Förderer und die erfolgte Förderung vergleichend zu beurteilen.
 Abb. 21a: Beispielhafte Aufgabenstellung zum Übergang Diagnose – Föderung
Abb. 21a: Beispielhafte Aufgabenstellung zum Übergang Diagnose – Föderung

Abb. 21b: Mögliche Berarbeitung
Schritt 2 der Reflexion: Übersicht über den Förderverlauf
Anhand der vorliegenden Dokumente verschaffen sich die Studierenden einen groben Überblick über den Verlauf der Förderungen und erstellen eine tabellarische Übersicht der Förderstunden mit Blick auf Indikatoren für Symptome und Basiskompetenzen zusammen: das sogenannte Förderfeld. Daran kann sich im nächsten Schritt die Frage anschließen, ob eine Entwicklung erkennbar ist.

Abb. 22a: Beispielhafte Aufgabenstellung zur ersten Reflexion einer Förderung
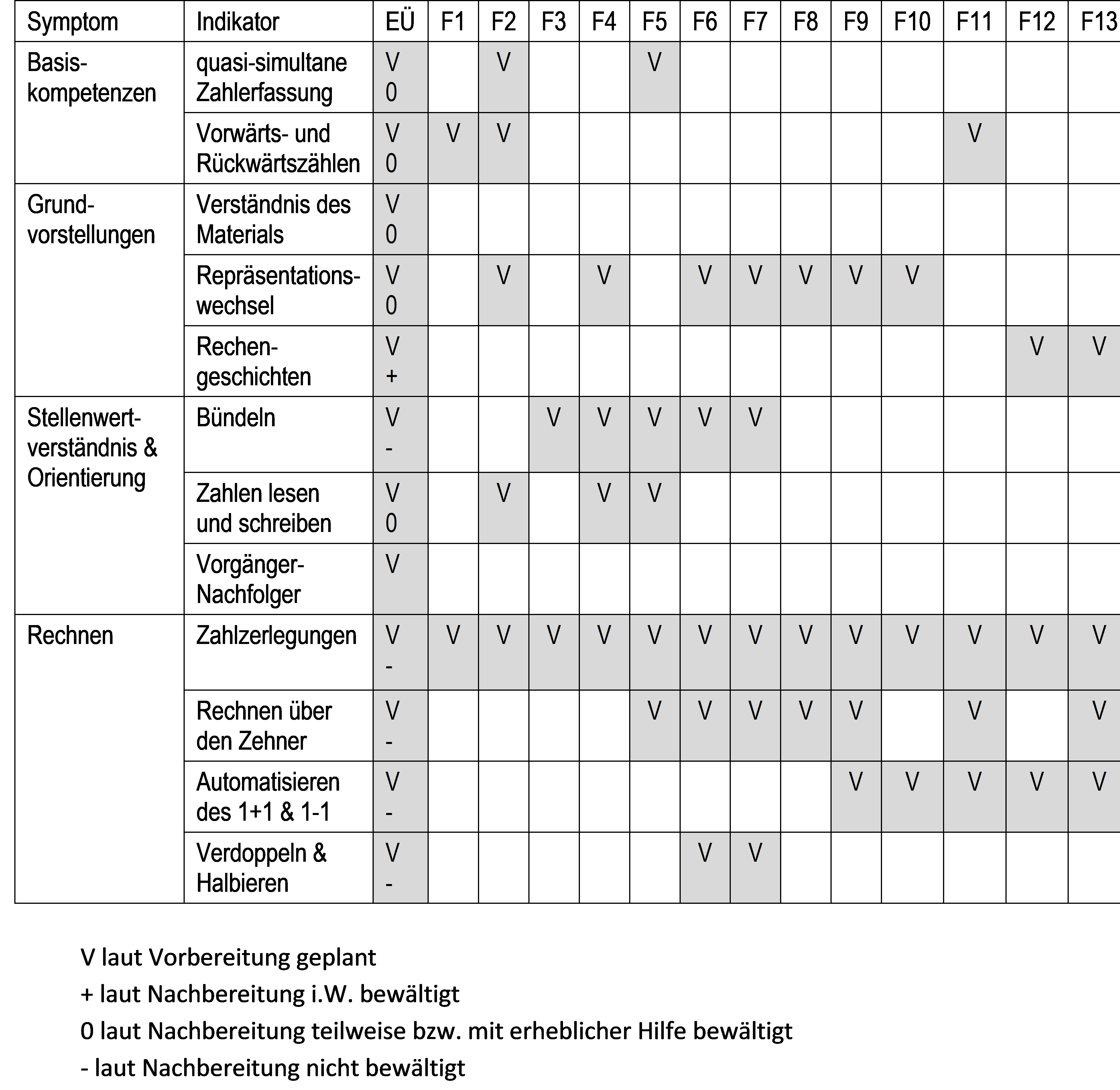
Abb. 22b: Erste Schritte der Bearbeitung

Abb. 22c: Beispielhafte Reflexion zum Förderfeld
Schritt 3 der Reflexion: Präzisierung von Fragestellungen an die Förderung und Auswahl von Methoden zur Bearbeitung
An eine Förderung lassen sich unterschiedliche vertiefende Fragen stellen. Diese lassen sich gliedern nach der Zielrichtung (Verlauf der Förderung oder Erfolg) und nach dem Grad der Offenheit:
Ziel 1: Überblick über den Verlauf der Förderungen – ist eine Entwicklung erkennbar? (offene Frage)
Dazu können die Förderübersicht und das Förderfeld genutzt werden. Eine sinnvolle Eingrenzung der Fragestellung auf der Basis des theoretischen Hintergrunds wird hier exemplarisch vorgenommen: Die Studierenden sollen hier erkennen, dass Ablösung vom Material als Entwicklungszeichen im Rahmen der Konzeption von Wartha & Schulz (2012) beschrieben werden kann als Aufsteigen im Vierphasenmodell.

Abb. 23: Beispielhafte Aufgabenstellung zur vertiefen Reflexion
Ziel 2: Hatte die Förderung Erfolg? (geschlossenere Fragen)
Dafür wurden im Seminarverlauf mit den Studierenden die folgenden Möglichkeiten zur Präzisierung der Fragestellung erarbeitet, um im Sitzungsverlauf Erfolg ablesbar zu machen:
- Beschreibung von Fördererfolg anhand des Aufstiegs im Phasenmodell bei inhaltlich vergleichbaren Aktivitäten ( z.B. Untersuchung aller Aktivitäten, die Strukturierung und Strukturerkennung von Zahlen fördern oder verwenden).
- Höherer Bearbeitungserfolg bei inhaltlich ähnlichen oder vergleichbaren Aufgaben auf derselben Stufe (z.B.: Zählen mit Material klappt nach einigen Sitzungen besser)
- Erfolg als wachsende Fähigkeit zum intermodalen Transfer: Episoden analysieren mit Diagrammen zum Grundvorstellungsumweg (GV-Diagramm).
Schritt 4 der Reflexion: Darstellung exemplarischer Ergebnisse der Arbeit an präzisierten Fragestellungen
Dieser Schritt erfolgt, um die Studierenden zur Umsetzung analoger Fragen bei der Reflexion der selbst durchgeführten Förderung anzuleiten. Wir wählen dazu bei Annika zunächst exemplarisch die 5. Förderstunde aus, da in dieser laut Förderfeld mit dem Rechnen über den Zehner begonnen wird. Es geht hier darum, sinnvolle Fragen an die Förderung zu stellen (wo sind interessante Stellen). Später können auf dieser Grundlage im Vergleich mit einer nachfolgenden Förderstunde auch begründete Aussagen über Entwicklungen getroffen werden. Wir greifen daraus hier nur einen Teilschritt heraus:

Abb. 24: Beispielhafte Aufgabenstellung zur genaueren Reflexion einer Förderaktivität
Aufgrund der Ergebnisse dieser Aufgabe wird folgende Episode aus diesem Förderschwerpunkt detaillierter analysiert und mit einer ähnlichen Aktivität aus der 11. Förderstunde verglichen im Hinblick auf eine mögliche Entwicklung:

Abb. 25a: Beispielhafte Aufgabenstellung zur Detailanalyse
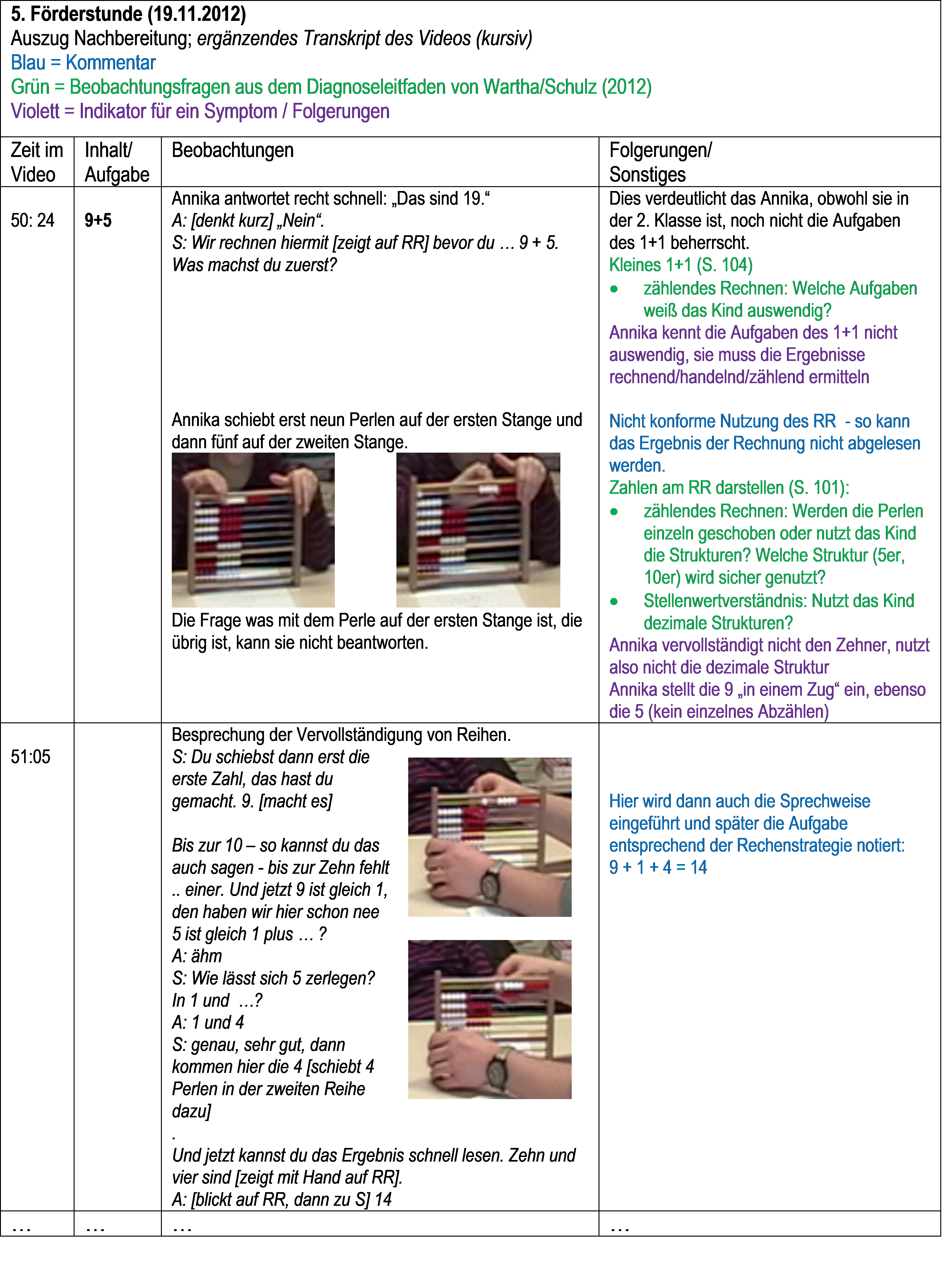
Abb. 25b: Auszug einer möglichen Detailanalyse einer Förderepisode (5. Förderung, 9+5)
Die Arbeit am Material lässt sich hier als Grundvorstellungsumweg deuten - allerdings gelingt dem Förderkind hier nur der erste Schritt, die weiteren werden vom Förderer vorgezeichnet und von Annika bloß nachvollzogen. Der Wechsel wird auch sichtbar in folgendem GV-Diagramm:
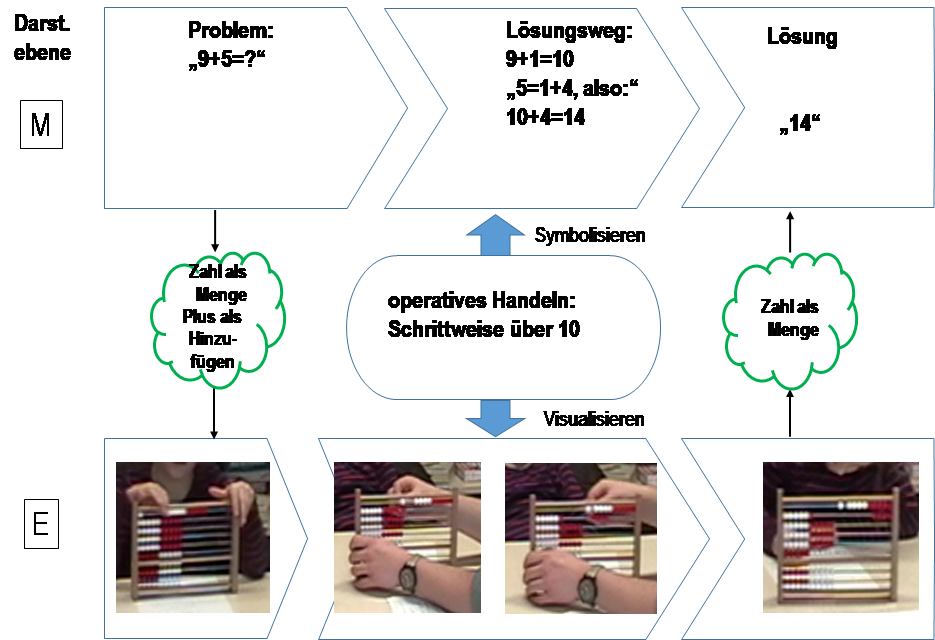
Abb. 25c: Grundvorstellungskreislauf einer Förderepisode (5. Förderung, 9+5)
Die Strukturbilder der Episode zeigen überwiegend Indikatoren für Rechenschwäche. Zur Darstellung wurde die oben erarbeiteten Strukturbilder angepasst: Ausgewählte Beobachtungen belegen die einschlägigen Indikatoren.
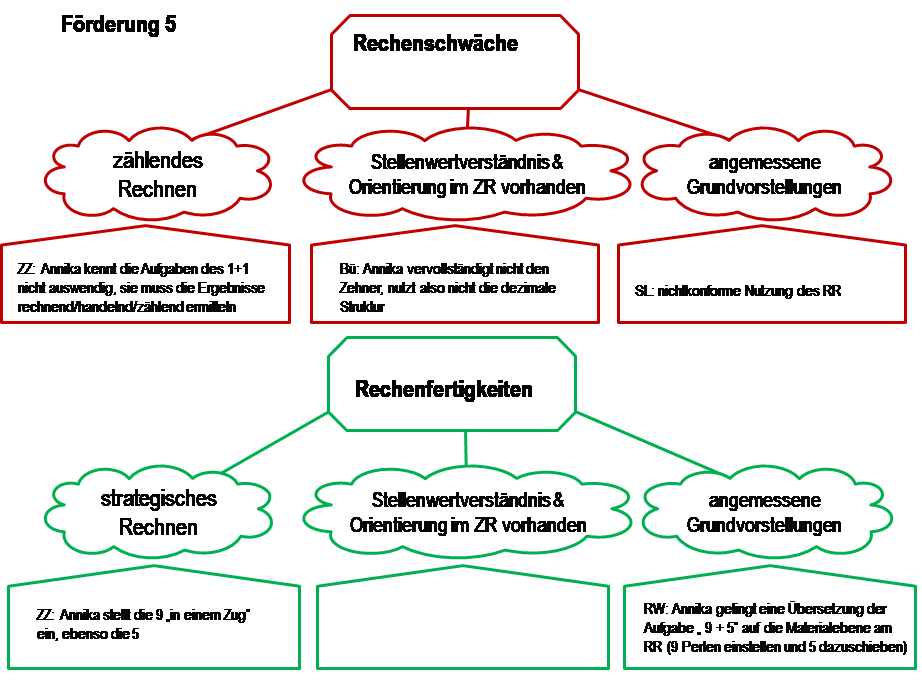
Abb. 25d: Strukturdiagramm zur Analysierten Förderepisode (5. Förderung, 9+5)
Um eine mögliche Entwicklung nachweisen zu können, wird eine vergleichbare Episode aus einer der letzten Förderstunden ausgewählt und analysiert:

Abb. 26: Detailanalyse einer ähnlichen Förderaktivität zum späteren Zeitpunkt (11. Förderung, 7+6)
In dieser Episode gelingt der Grundvorstellungsumweg besser: Die Hürde besteht hier nicht mehr aufgrund eines Verstehens-, sondern aufgrund eines Gedächtnisproblems. Der Fördererfolg wird auch in den Strukturbildern sichtbar durch die veränderte Indikatorenzusammensetzung:

Abb. 27: Detailanalyse im Strukturdiagramm (11. Förderung, 7+6)
Die Episode zeigt auch, dass Annika beginnt, sich vom Material abzulösen: Die Antwort in 4:20 liest sie nicht mehr am Rechenrahmen ab, sondern hat sie „im Kopf“. Passend dazu wird anschließend in Phase 3 statt Phase 2 gefördert. Im Vergleich zu der Episode aus Förderstunde 5, die in Phase 1 nicht zum Erfolg führte, ist hier eine deutliche Entwicklung erkennbar. Weitere Episoden aus dieser Förderung zeigen indes, dass dieser Erfolg eher punktuell ist.
Schritt 5 der Reflexion: Diskussion der Ergebnisse
Hier werden die im Rahmen der Bearbeitung gefundenen Analyseresultate einander gegenübergestellt (sinnvolle Kontraste: Förderverlauf vs. Vorher-Nachher-Vergleich, Strukturbilder von Interview und BIRTE-Testung vs. Förderepisoden, eigene Befunde vs. Förderplanung und Abschlussbericht der Förderer) und zur Literatur in Beziehung gesetzt. Beispielweise zeigt sich durch das bessere Gelingen von Grundvorstellungsumwegen ein Fördererfolg auf der Verstehensebene: „Ein Verständnis des mathematischen Inhalts wird dann unterstellt, wenn eine Lösung auch über die Aktivierung von Grundvorstellungen in einer anderen Darstellung möglich ist.“ (Wartha & Schulz 2012, 39)
5.6 Ausblick
Im Rahmen der DuF-Seminare werden zunächst die Arbeitsweisen bei der Diagnostik und Förderung erlernt (DuFp), dann in der eigenen Förderungen erprobt (DuFq) sowie anschließend reflektiert (DuFr). Zur synoptischen Falldarstellung und -konstrastierung sind dabei insbesondere zwei Werkzeuge nutzbar, die wir hier (wie im Seminar) anhand der Analyse und Beurteilung der Förderung von Annika erläutert haben:
- Strukturbilder zur übersichtlichen Präsentation auftretender Indikatoren von Rechenschwäche bzw. -fertigkeit , um entweder einzelne Förderepisoden lokal oder die Diagnostik vor bzw. nach erfolgter Förderung global zu vergleichen,
- GV-Diagramme zur Beschreibung von Grundvorstellungsumwegen, die nach Wartha & Schulz (2012) als Verständnisindikator“ dienen, womit ein Förderfolg durch zunehmend gelingende Umwege angezeigt werden kann ‒ und ebenso durch ein Fortschreiten im Vierphasenmodell.
Auch in der späteren Berufspraxis können die angehenden Lehrkräfte diese Werkzeuge nutzen, um Förderverläufe und -entscheidungen methodisch sauber zu beurteilen. Diese Verschränkung des wissenschaftlichen mit dem praktisch-pädagogischen Habitus nach Blömeke scheint uns nützlich sowohl im Hinblick auf die Selbstreflexion der eigenen Förderpraxis als auch im Hinblick darauf, dass Lehrkräfte zunehmend per Gutachten über das (Fort-)Bestehen von Förderbedarf zu entscheiden haben.
6. Literatur
Baumert, J., Bos, W. & Lehmann, R. H. (Hrsg.,2000). TIMSS/III: Dritte Internationale Mathematik- und Naturwissenschaftsstudie – Mathematische und naturwissenschaftliche Bildung am Ende der Schullaufbahn, Bd. 1. Opladen: Leske + Budrich.
Baumert, J., Klieme, E., Neubrand, M., Prenzel, M., Schiefele, U., Schneider, W., Stanat, P., Tillman, K.-J., & Weiß, M. (Hrsg.,2001). PISA 2000: Basiskompetenzen von Schülerinnen und Schülern im internationalen Vergleich. Opladen: Leske & Budrich
Bikner-Ahsbahs, A.; Große Kamphake, L.; Büssing, J.; Dittmer, J.; Wieferich, A.: Mathematikunterricht inklusiv gestalten: Die Drei-Elemente-Methode - In: Beiträge zum Mathematikunterricht 2016 Münster: WTM-Verlag 149 – 152, Abgerufen am 4.9. 2017 von https://eldorado.tu-dortmund.de/bitstream/2003/35278/1/BzMU16%20BIKNER%20Inklusiv.pdf
BLK (Bund-Länder-Kommission für Bildungsplanung und Forschungsförderung, Projektgruppe „Innovationen im Bildungswesen“, Hrsg.,1997). Gutachten zur Vorbereitung des Programms „Steigerung der Effizienz des mathematisch-naturwissenschaftlichen Unterrichts“. Abgerufen am 4.9. 2017 von http://www.blk-bonn.de/papers/heft60.pdf.
Blömeke, S. (2001). Erwerb professioneller Kompetenz in der Lehrerausbildung und die Aufgabe von Zentren für Lehrerbildung. In: Seibert, N. (Hrsg.): Probleme der Lehrerbildung. Bad Heilbrunn: Klinkhardt, 131-162
Breidenbach, W. (1966). Raumlehre in der Volksschule: eine Methodik. Hannover: Schroedel.
Feuser, G. (1998): Gemeinsames Lernen am gemeinsamen Gegenstand. Didaktisches Fundamentum einer Allgemeinen (integrativen) Pädagogik. In Hildeschmidt, A./ Schnell, I. (Hrsg.): Integrationspädagogik. Weinheim: Juventa. 19-36.
Freudenthal, H. (1983). Didactical Phenomenology of Mathematical Structures. Dordrecht: Kluwer .
Gaidoschik, M. (2016). Prävention von „Rechenschwächen“: Was Fachdidaktik kann und könnte. - In: Beiträge zum Mathematikunterricht 2016 Münster: WTM-Verlag
Gaidoschik, M. , Deweis, K.M. & Guggenbichler, S. (2017). How lower-achieving children cope with derived facts-based teaching of basic multiplication. Proceedings of CERME 10. Abgerufen am 4.9. 2017 von https://keynote.conference-services.net/resources/444/5118/pdf/CERME10_0356.pdf
Gemeinsame Kommission Lehrerbildung von DMV, GDM, MNU (2017): Fachdidaktik für den inklusiven Mathematikunterricht – Orientierungen und Bemerkungen. Mitteilungen der Gesellschaft für Didaktik der Mathematik, 42(103), 42-46. Abgerufen am 4.9. 2017 von http://ojs.didaktik-der-mathematik.de/index.php/mgdm/article/view/95
Gillen, J. (2015): Das Leibniz-Prinzip in der Lehrerbildung. Unimagazin 3/4, 14-19. http://bit.ly/2rfq9Qc
Heymann, H.-W. (1996). Allgemeinbildung und Mathematik. Weinheim: Beltz.
Häsel-Weide, U./Nührenbörger, M. (2013): Mathematiklernen im Spiegel von Heterogenität und Inklusion. – In: Mathematik differenziert, 4(2), 6 – 8.
Höveler, K., & Prediger, S. (2017). Vielfältige Rechenwege finden, erläutern und begründen. Gemeinsames Lernen in inklusiven Klassen inszenieren. In mathematik lehren, Heft 201, 11-16.
Jahnke, Th. (2010). Vom mählichen Verschwinden des Fachs aus der Mathematikdidaktik. Mitteilungen der GDM, 89, 21-24.
Jahnke, T., Klein, H. P., Kühnel, W., Sonar, T., & Spindler, M. (2014). Die Hamburger Abituraufgaben im Fach Mathematik. Mitteilungen der DMV, 22, 115-121.
Karaschewski, H. (1966). Wesen und Weg des ganzheitlichen Rechenunterrichts. Stuttgart: Klett.
Käpnick, F. (2016): Verschieden verschiedene Kinder. Inklusives Fördern im Mathematikunterricht der Grundschule. Seelze: Kallmeyer.
Keitel, C., & Vithal, R. (2008). Mathematical power as political power–the politics of mathematics education. In Clarkson, P., & Presmeg, N. C. (Hrsg.): Critical issues in mathematics education. Berlin: Springer, 167-188
Klieme, E., Avenarius, H., Blum, W., Döbrich, P., Gruber, H., Prenzel, M., et al. (2003). Zur Entwicklung nationaler Bildungsstandards. Berlin: Bundesministerium für Bildung und Forschung
Klieme, E., Artelt, C., Hartig, J., Jude, N., Köller, O., Prenzel, M., & Wolfgang, S. (Eds.). (2010). PISA 2009: Bilanz nach einem Jahrzehnt. Waxmann
Korff, N. (2015). Inklusiver Mathematikunterricht in der Primarstufe. Erfahrungen, Perspektiven und Herausforderungen. Hohengehren: Schneider
Krummheuer, G. (2013). The relationship between diagrammatic argumentation and narrative argumentation in the context of the development of mathematical thinking in the early years. Educational Studies in Mathematics, 84(2), 249-265.
Krummheuer, G. (1995). The ethnography of argumentation. In P. Cobb & H. Bauersfeld (Hrsg.), The emergence of mathematical meaning: Interaction in classroom cultures. Hillsdale: Lawrence Erlbaum, 229-269
Leuders, T. (2011): Kompetenzorientierung – eine Chance für die Weiterentwicklung des Mathematikunterrichts? In: Eilerts, K.; Hilligus, A. H.; Kaiser, G. & Bender, P. (Hrsg.) Kompetenzorientierung in Schule und Lehrerbildung. Münster: LIT, 287-306.
Leuders, T.,Prediger, S. (2016): Flexibel differenzieren und fokussiert fördern im Mathematikuntericht. Berlin: Cornelsen.
Lesh, R., & Sriraman, B. (2005). Mathematics education as a design science. Zentralblatt für Didaktik der Mathematik, 37(6), 490-505.
Mayring, Philipp (2008). Qualitative Inhaltsanalyse. Weinheim: Beltz.
Meyerhöfer, W. (2011). Vom Konstrukt der Rechenschwäche zum Konstrukt der nicht bearbeiteten stofflichen Hürden. Pädagogische Rundschau, 65(4), 401-426.
Neumann, K., Fischer, H. E., & Kauertz, A. (2010). From PISA to educational standards: The impact of large-scale assessments on science education in Germany. International Journal of Science and Mathematics Education, 8(3), 545-563.
Niedersächsisches Kultusministerium (2009). Kerncurriculum für das Gymnasium – Mathematik 2009. Online abrufbar unter http://db2.nibis.de/1db/cuvo/datei/kc_mathematik_go_i_2009.pdf.
Rasch, R. (2016): Differenzieren und Fördern im Mathematikunterricht –Rechenschwäche / Rechenstörung / Dyskalkulie. Abgerufen am 13.9.2017 von http://docplayer.org/29268175-8-3-differenzieren-und-foerdern-im-mathematikunterricht-rechenschwaeche-rechenstoerung-dyskalkulie-klaerung-von-begriffen-diskussion-von-ursachen.html
Reiss, K. & Ufer, S. (2009). Fachdidaktische Forschung im Rahmen der Bildungsforschung. Eine Diskussion wesentlicher Aspekte am Beispiel der Mathematikdidaktik. In: R. Tippelt & B. Schmidt (Hrsg.), Handbuch Bildungsforschung, 199-213. Wiesbaden: VS-Verlag.
Schipper, W. (2005a). Rechenstörungen als schulische Herausforderung: Basispapier zum Modul G4: Lernschwierigkeiten erkennen - verständnisvolles Lernen fördern. Kiel: IPN.
Schipper, W. (2005b). Übungen zur Prävention von Rechenstörungen. In: Die Grundschulzeitschrift, 19, H. 182. (Download unter: http://www.bielefelder-rechentest.de/ftp/Förderkartei.pdf)
Schipper, W. (2008). Handreichung zur Förderung von Kindern mit besonderen Schwierigkeiten beim Rechnen. Bielefeld.
Schipper, W. (2009). Handbuch für den Mathematikunterricht an Grundschulen. Hannover: Schroedel
Schipper, W., Wartha, S. & von Schroeders, N. (2011). BIRTE 2, Bielefelder Rechentest für das 2. Schuljahr. Hannover: Schroedel.
Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland (KMK, Hrsg.). (2004). Bildungsstandards im Fach Mathematik für den Mittleren Schulabschluss. München: Luchterhand
Steinbring, H. (1998): Mathematikdidaktik: Die Erforschung theoretischen Wissens in sozialen Kontexten des Lernens und Lehrens. Zentralblatt für Didaktik der Mathematik (1998) 30, 161-167
Tenorth, H.-E. (2011): „Bildung“ – ein Thema im Dissens der Disziplinen. Zeitschrift für Erziehungswissenschaft, 14(3), 351–362.
Tenorth, E. (Hrsg., 2010): Mathematik entlang der Bildungskette. Empfehlungen einer Expertengruppe zur Kompetenzentwicklung und zum Förderbedarf im Lebenslauf. Bonn: Deutsche Telekom Stiftung.
Voigt, J. (1994): Entwicklung mathematischer Themen und Normen im Unterricht. – In: H.Maier; J. Voigt (Hg.), Verstehen und Verständigung im Mathematikunterricht – Arbeiten zur interpretativen Unterrichtsforschung. Köln: Aulis, 77–111.
Vom Hofe, R. (1995) Grundvorstellungen mathematischer Inhalte. Heidelberg: Spektrum.
Wartha, S., Schulz, A. (2011). Aufbau von Grundvorstellungen (nicht nur) bei besonderen Schwierigkeiten im Rechnen. Kiel: IPN-Materialien.
Wartha, S., Schulz, A. (2012): Rechenproblemen vorbeugen. Berlin: Cornelsen
Weltgesundheitsorganisation WHO (2014). Internationale Klassifikation psychischer Störungen: ICD-10 Kapitel V (F) Klinisch-diagnostische Leitlinien (9. Aufl.). Bern: Huber.
Winter, H. (1995). Mathematikunterricht und Allgemeinbildung. Mitteilungen der Gesellschaft für Didaktik der Mathematik, 61, 37–46.
Wittmann, E.Ch. (2014). Die Ideologie der Selbstbeschränkung in der Mathematikdidaktik. Mitteilungen der GDM, 96, 15–19













 Abb. 13: Das Leibnizprinzip in der Lehrerbildung (Gillen 2015)
Abb. 13: Das Leibnizprinzip in der Lehrerbildung (Gillen 2015)








 Abb. 21a: Beispielhafte Aufgabenstellung zum Übergang Diagnose – Föderung
Abb. 21a: Beispielhafte Aufgabenstellung zum Übergang Diagnose – Föderung 










