
Abb. 1: Bauteile des Exhibits „Ei des Kolumbus“
Der grundlegendste Zugang zu diesem Exhibit ist das haptische Wahrnehmen der einzelnen Teile.
Lederman und Klatzky (1987) identifizieren folgende Erkundungsprozeduren (exploratory procedures)
Abstract: Im Rahmen des Entwicklungsprojekts HdMa on tour (Haus der Mathematik on tour) zum entdeckenden Lernen mathematischer Problemstellungen mit interaktiven Exponaten haben wir nach differenzierten Lernzugängen gesucht. Diese erweiterten Lernzugänge sollten eine niedrigschwellige und dennoch entdeckende Herangehensweise für Kinder mit unterschiedlichen Lernvoraussetzungen ermöglichen und somit die Individuallage der Kinder berücksichtigen. Schwierigkeiten auf Grund von heterogenen sprachlichen Voraussetzungen wurden berücksichtig, indem ein neuer Ansatz mit zusätzlichen grafischen Anleitungskärtchen umgesetzt wurde. Um die Problemlösekompetenz im entdeckenden Lernen im Lernprozess der Kinder zu fördern wurden Rahmen als Orientierungshilfen konzipiert. Zusätzlich entwickelten wir visuelle Wahrnehmungshilfen, um den Kindern differenzierte Lernzugänge auf unterschiedlich komplexen Entdeckungsebenen anzubieten. In dieser Arbeit präsentieren wir die Weiterentwicklung der HdMa on tour und machen die didaktische Systematik, der wir gefolgt sind, nachvollziehbar.
Stichworte: Hands on, Science Center, Differenzierung, entdeckendes Lernen, Mathematik, strukturierende Lernhilfen
Inhaltsverzeichnis
HdMa on tour (Haus der Mathematik on tour) ist eine Wanderausstellung von interaktiven Ausstellungsobjekten mit Schwerpunkt Mathematik, das von Lehrenden der PH Wien entwickelt wurde und Lehrerinnen und Lehrern, Schülerinnen und Schülern in ganz Österreich zur Verfügung steht. An dreißig verschiedenen Stationen (Exhibits) kann man Mathematik an-greifen und dadurch idealerweise auch be-greifen. Durch eigenständiges und aktiv-entdeckendes Experimentieren, verbunden mit entsprechenden Anregungen zum Nachdenken, sollen den Schülerinnen und Schülern mathematische Zusammenhänge und Phänomene nahegebracht werden. Entsprechend der Philosophie, Mathematik haptisch erlebbar zu gestalten, also durch eigene Handlungen erfahrbar zu machen, wurden in einigen Exhibits mathematische Problemstellungen be-greifbar gemacht und fordern zum entdeckenden Lernen auf. In anderen Exhibits wurde der Schwerpunkt auf das Erkennen von Strategien gelegt. Als Hauptzielgruppe waren ursprünglich Kinder im Alter von 10 bis 14 Jahren angedacht.
Die einzelnen Exhibits sind grundsätzlich so konzipiert, dass sie eine niedrige Einstiegsschwelle in das Entdecken von Mathematik bieten. Die sehr heterogenen Gruppen im Schulalltag und der inklusive Gedanke, erfordern allerdings eine noch differenziertere Herangehensweise. Es hat sich gezeigt, dass jüngere Kinder, Kinder mit besonderen Bedürfnissen oder Kinder mit mangelnden sprachlichen Kenntnissen teilweise einen noch grundlegenderen und voraussetzungsloseren Zugang brauchen. Die Idee, HdMa on tour in diesem Sinne noch weiter zu öffnen, haben wir aufgegriffen und zeigen hier, welche Differenzierungsmaßnahmen an einzelnen Exhibits gesetzt werden können und wie diese in Lehr/Lernarrangements bei der Arbeit mit den Exhibits eingesetzt werden können.
In der Mathematik geht es darum, Muster, Strukturen, Regelmäßigkeiten, Beziehungen wahrzunehmen, zu erkennen, zu beschreiben, zu nutzen, zu erkunden, zu verstehen. Dieser Zugang zur Mathematik wird von Keith Devlin so beschrieben:
„Mathematik ist die Wissenschaft von Mustern. Der Mathematiker untersucht abstrakte ‚Muster‘ – Zahlenmuster, Formenmuster, Bewegungsmuster, Verhaltensmuster und so weiter. Solche Muster sind entweder wirkliche oder vorgestellte, sichtbare oder gedachte, statische oder dynamische, qualitative oder quantitative, auf Nutzen ausgerichtet oder bloß spielerischem Interesse entspringende.“ (Devlin und Diener 2002, S. 3–4)
Dieser Zugang zur Mathematik soll nicht den Fachmathematikerinnen und Fachmathematikern überlassen werden. Diesen gilt es den Schülerinnen und Schülern zu vermitteln, nur so können sie die Mathematik von ihrem Wesen aus entdecken. Somit bietet sich den Schülerinnen und Schülern weder ein rein pädagogischer oder rein mathematischer, sondern eben ein pädagogisch-mathematischer Zugang zur Mathematik. Alle Kinder sollen sich aktiv, interaktiv auf entdeckende Weise die Welt der Muster – also die Mathematik – erschließen. Um dies für alle Kinder möglich zu machen, muss von der Sache aus zuerst differenziert werden, um so das Konzept der natürlichen Differenzierung, wie es von Wittmann entwickelt wurde, zu ermöglichen. Wittmann erkennt die Bedeutung von entsprechenden Lernangeboten:
„Der Schlüssel dafür liegt in Lernangeboten, die eine niedrige Eingangsschwelle haben, einen bestimmten Grundbestand von Kenntnissen und Fertigkeiten sichern und darüber hinaus den Kindern Optionen ermöglichen, die sie nach ihren individuellen Möglichkeiten wahrnehmen können “ (Wittmann 2010, S. 63)
Das Prinzip von der natürlichen Differenzierung, d.h. der Differenzierung vom Kind aus, bietet somit optimale Möglichkeiten, um Kinder mit unterschiedlichen Voraussetzungen im gemeinsamen Unterricht individuell zu fördern. Die Lernangebote müssen dabei so reichhaltig angelegt sein, dass sie jedes Kind quer über das gesamte Leistungsspektrum für seine Fortschritte nutzen kann und in seinem individuellen Lerntempo den Tiefengrad der Komplexität in der Problemstellung bestimmen kann. Als Basis für dieses gemeinsame Lernangebot werden Lernumgebungen gesehen:
„Eine Lernumgebung ist eine flexible große Aufgabe. Sie besteht in der Regel aus mehreren Teilaufgaben und Arbeitsanweisungen, die durch bestimmte Leitgedanken - immer basierend auf einer innenmathematischen oder sachbezogenen Struktur - zusammengebunden sind.“(Hengartner et al. 2010, S. 9)
Lernumgebungen erlauben eine Zugänglichkeit für alle Lernenden, und regen darüber hinaus zu einem sozialen Austausch und zum Kommunizieren über Mathematik an.
Die HdMa on tour besteht aus 30 Exhibits. Als “Exhibit” definiert McLean interaktive Ausstellungsobjekte “... in which visitors can conduct activities, gather evidence, select options, form conclusions, test skills, provide input, and actually alter a situation based on input.” (McLean 1996, S. 93)
Alle von ihnen beinhalten PAR-interaktive Grundzüge, d.h. sie sind „physical“ (angreifbar, materiell), „adjustable“ (anpassbar, verstellbar) und „relevant“ (bedeutungsvoll für das zu zeigende Phänomen) (vgl. Allen und Gutwill 2004).
Die Exhibits der HdMa on tour sind in sich kleine Lernumgebungen. Sie versuchen mathematische Muster (Ideen) angreifbar, begreifbar und somit sichtbar zu machen.
„A mathematics manipulative material is an object that can be handled by an individual in a sensory manner during which conscious and unconscious mathematical thinking will be fostered.“ (Swan und Marshall 2010, S. 14)
In einigen Studien wurde gezeigt, dass für junge, aber auch gerade für lernschwache Schülerinnen und Schüler und für Kinder mit mangelnden Sprachkenntnissen der Einsatz von mathematischem, „manipulativem Material“ das Verstehen fördern kann. (vgl. Cope 2015, Rosli et al. 2015 oder auch Siew et al. 2013) Das manipulative Material ist hier im Sinne eines Materials zu verstehen, das zum (Nach-)Entdecken von mathematischen Inhalten, durch Forschungsaufträge angeleitet, anregt.
Ein aktiv entdeckender Mathematikunterricht für alle Kinder, mit unterschiedlichsten Begabungen, egal ob mit ausgezeichneten oder nur geringen Deutschkenntnissen, egal ob alt oder jung bedeutet aber nicht, Kindern „lediglich Freiräume zum Entdecken und Produzieren zu eröffnen“ (Wember 2005, S. 285). Kindern muss gezielt Hilfestellung gegeben werden, so dass sie in einer Lernumgebung, die für sie wesentlichen Inhalte erarbeiten können.
Aber welche Merkmale einer Aufgabe sind schwierigkeitsgenerierend? Hußmann und Prediger (2007, S. 3) nennen unter anderem die folgenden:
Damit auch für lernschwache Schülerinnen und Schüler eine aktive Auseinandersetzung mit dem Lerngegenstand ermöglicht wird, bedarf es einer Entschärfung dieser schwierigkeitsgenerierenden Merkmale. Heimlich und Wember (2012, S. 75) nennen dazu strukturierende Lernhilfen, lernbegleitende Anleitung, lehrerzentrierte Elemente als Möglichkeiten. Scherer und Moser Opitz (2010, S. 52) weisen darauf hin, dass für einen offenen Unterricht für leistungsschwache Schülerinnen und Schüler strukturierende Lernhilfen (adaptiertes Unterrichtsmaterial, klare Instruktion) unabdingbar für einen Lernzuwachs zu sein scheinen.
Ziel dieser strukturierenden Lernhilfen ist es, die Schwierigkeiten zu reduzieren. Sie können verringert werden, indem man eine vereinfachte Sprache einsetzt, bildliche Hinweise gibt oder Lösungsbeispiele vorgibt. Aber auch eine Anpassung des Materials an sich, kann gezielt Schwierigkeiten entschärfen. Wie wir diese Forschungsergebnisse umsetzen, zeigen wir im nächsten Abschnitt an einigen Exhibits exemplarisch.
In den Forschungsergebnissen wird aber auch immer darauf hingewiesen, dass die Lehrkraft eine essentielle Rolle einnimmt:
„To be effective, however, simply placing one’s hands on the manipulative materials will not magically impart mathematical understanding. Without the appropriate discussion and teaching to make the links to the mathematics explicit, the very opposite may be true; children may end up with mathematical misconceptions.“ (Swan und Marshall 2010, S. 19)
Um gemeinsames Mathematiklernen für alle Kinder zu ermöglichen, bedarf es einer gezielten Vorbereitung eines Lehr/Lernarrangements durch die Lehrkraft. Damit ist gemeint, dass ein Lernprozess vom Lehrenden bewusst unter bestimmten didaktisch-methodischen und sozial-interaktiven Gesichtspunkten zu gestalten ist. Da geht es einerseits um die inhaltliche Auswahl aber auch um die Inszenierung an sich. Mathematiklernen ist unter anderem ein kommunikativer Prozess, es geht also auch um einen inhaltlichen Austausch mit den anderen Kindern, mit der Lehrperson.
„Guter inklusiver Mathematikunterricht bewegt sich in einem Spannungsfeld von individueller Förderung jedes einzelnen Kindes mit seinen Besonderheiten und dem gemeinsamen Lernen aller Kinder eines Klassenverbandes.“ (Häsel-Weide 2015, S. 191)
Eine gezielte Vorbereitung eines Lehr/Lernarrangements ist also unerlässlich, welche Möglichkeiten HdMa on tour – differenziert bietet, wird im Abschnitt Lehr/Lernarrangements erläutert.
Anhand charakteristischer Exhibits sollen die von uns entwickelten Differenzierungsmöglichkeiten in diesem Abschnitt erläutert werden und Designentscheidungen diskutiert werden.
Wir betrachten ein Exhibit („Ei des Kolumbus“), das sich mit der Geometrie der Ebene befasst, weitere Exhibits („T-Würfel“, „Natürliche Zahlen Würfel“), wo Ideen der Raumgeometrie aufgegriffen werden, ein Exhibit („Dudeney’s Zerschneidung“), bei dem es um Flächeninhaltsgleichheit geht, und ein Exhibit („Nim Spiel“), das das Entdecken von Strategien bei einem Spiel zum Ziel hat.
Das Exhibit „Ei des Kolumbus“ ist eine Variante des Tangram Spiels, bei dem es darum geht aus neun Teilen eine Form, nämlich ein Ei zu legen.

Abb. 1: Bauteile des Exhibits „Ei des Kolumbus“
Der grundlegendste Zugang zu diesem Exhibit ist das haptische Wahrnehmen der einzelnen Teile.
Lederman und Klatzky (1987) identifizieren folgende Erkundungsprozeduren (exploratory procedures)
Durch die letztgenannte Prozedur kann aufgrund der Wahrnehmung eine Sortierung bzw. Klassifizierung der einzelnen Teile stattfinden. Die Kriterien, nach denen sortiert wird sind vielfältig. So z.B. können in einem ersten Schritt gleiche Teile gefunden werden oder in große und kleine Teile sortiert werden. In einem weiteren Schritt gilt es die Teile aufgrund der Anzahl der Ecken zu sortieren oder in Teile, die nur gerade Kanten aufweisen und in solche, die von geraden und kreisförmigen Strukturen begrenzt sind. Die Tätigkeit des Sortierens und Klassifizierens ist eine mathematische Grunderfahrung, an diese Erfahrung knüpft die Stärkung der sprachlichen Ausdrucksfähigkeit: Die Erfahrungen und Ideen werden sprachlich formuliert, um so einen Austausch untereinander zu ermöglichen.
Das Ziel des Exhibits in der ursprünglichen Form ist das Legen einer geometrischen Form. Aber schon das Auslegen bzw. Nachlegen dieser geometrischen Form fordert eine abstrakte geometrische Denkleistung. Gemäß des van Hiele Modells (vgl. Crowley 1987) erfolgt die Entwicklung des geometrischen Denkens in mehreren Stufen mit fortschreitender Abstraktion. Die nullte Niveaustufe (Grundniveau) beinhaltet das räumliche anschauungsgebundene Denken („visualization“), in der geometrische Objekte als Ganzes wahrgenommen werden, Bestandteile und Eigenschaften noch nicht erkannt werden, das Denken an das Hantieren mit Material gebunden ist. Das Legen bzw. das Auslegen von Figuren lässt sich dieser Stufe, dem anschauungsgebundenen Denken, zuordnen.
Will man dieses Legespiel nun tatsächlich legen, so bietet das Exhibt der HdMa on tour folgende gestuften Differenzierungsmaßnahmen an:
Die ursprüngliche Version der HdMa on tour arbeitet mit Anleitungskärtchen, auf denen der Arbeitsauftrag in verbaler Weise präsentiert wird, kombiniert mit einem Forschungsauftrag, siehe Abb. 4 und dem entsprechenden Legematerial aus Holz. Um sprachlich keine Hürde, durch die Komplexität der Sätze, aufzubauen, war ein erster Schritt in Richtung Differenzierung und Inklusion eine Anleitungskarte ohne Text auszuprobieren. Dies würde jüngeren Schülerinnen und Schülern, Kindern mit Leseschwierigkeiten bzw. Kindern mit einer anderen Erstsprache als Deutsch entgegenkommen:
 Abb. 2 Anleitungskarte Ei des Kolumbus |
|
|
Auf den Anleitungskarten ohne Text wird versucht, allein durch piktographische, bildliche Umsetzung das Ziel der Aufgabenstellung den Schülerinnen und Schülern zugänglich zu machen.
Die Forschungsaufträge, die sich auf den ursprünglichen Anleitungskarten befinden, müssen aber nicht unbeachtet bleiben: Die Lehrkraft kann im direkten Dialog mit dem Kind diese Fragen aufwerfen und gemeinsam versuchen zu beantworten.
Nach der Entwicklung von Anleitungskarten ohne Text, war die Frage spannend, wie auf der enaktiven Ebene Aspekte der Differenzierung beachtet werden können. In der ursprünglichen Version der HdMa on tour erkunden die Kinder das Exhibit nur mit der Anleitung auf den Karten und den zugehörigen Legeteilen. Es kann aber der Fall sein, dass dieses freie Explorieren vom Kind aus nicht möglich ist bzw. nicht gewünscht ist. Daher werden methodisch Schülerinnen und Schülern in der Weiterentwicklung der Exhibits nun als Orientierungshilfe Holzrahmen mit einer Vertiefung angeboten. Die Vertiefung zeigt den Rand der Figur und gibt somit Hinweis auf die fertige Figur. Durch diesen Holzrahmen als Orientierungshilfe erhält das Kind Anhaltspunkte auf der enaktiven und ikonischen Ebene. Der Holzrahmen gibt aufgrund seiner Rahmeneigenschaft sofort Rückmeldung, ob das Teil an der richtigen Stelle positioniert wurde. Der Rahmen ist bei weitem noch keine eindeutige schematische Vorgabe, die durch die Schülerinnen und Schüler ohne eigene Denkwege ausgelegt wird, sondern erfordert weiterhin ein problemlösekompetentes Herangehen an das Auffinden einer Lösung. Die unterschiedlichen Auslegemöglichkeiten müssen noch gefunden, erprobt und begründet werden. Falls ein noch freieres Explorieren vom Kind aus möglich bzw. gewünscht ist, könnte man sogar auch auf den Rahmen verzichten.

Abb. 4 Vertiefung "Ei des Columbus"
Als weitere Hilfestellung kann in den Holzrahmen ein „vollständiges Einlageblatt“ verwendet werden, dem alle Konturen der Teile zu entnehmen sind, siehe Abb. 5. Lernziele, die hier beim Legen der Figur gefördert werden, zielen vornehmlich auf visuelle Wahrnehmungsfähigkeiten, auf das Erkennen geometrischer Figuren, auf das Modellieren von ebenen Körpern beim Zusammenfügen der einzelnen Teile. Diese Hilfe erscheint uns den Komplexitätsgrad des Exhibits am meisten zu vereinfachen, um dem inklusiven Anspruch für möglichst viele Kinder gerecht zu werden.
Will man Schülerinnen und Schüler dazu anhalten, dass sie Eigenschaften der Achsensymmetrie erkennen und diese nutzen, so kann man ihnen den Holzrahmen mit einem Einlageblatt, das nur eine teilweise angeführten Konturstruktur der einzelnen Legeteile aufweist, zur Verfügung stellen, siehe Abb. 6.
|
|
|
Was allen Versionen gemeinsam ist, ist, dass dabei Legestrategien entwickelt werden müssen, ein systematisches Vorgehen geplant werden kann und darüber reflektiert werden sollte.
Eine mögliche Strategie ist es, mit den Teilen zu beginnen, die einen Kreisbogen als Begrenzung haben. Diese sechs Teile müssen so gelegt werden, dass sich die Ei-Form ergibt. Hat man das gemeistert, so müssen nur noch die drei Dreiecke eingepasst werden.
Bei den Würfel – Exhibits geht es darum, aus einzelnen Teilen einen Würfel zusammenzusetzen. Jedes einzelne Teil ist dabei selbst ein Polywürfel, d.h. es ist selbst aus kleineren jeweils identischen Einheitswürfeln zusammengesetzt. Insgesamt besteht jeder Würfel aus 3·3·3 = 33 = 27 Einheitswürfel.
Die unterschiedliche Zusammensetzung der Bauteile macht den Reiz dieser vielfältigen Würfel – Exhibits aus. Beim T-Würfel sind es zum Beispiel sechs mal 4 Einheitswürfel, die jeweils zu einem T angeordnet sind, und einem Quader bestehend aus 3 Einheitswürfeln. Beim „natürliche Zahlen Würfel“ bestehen die Bauteile aus unterschiedlich vielen Einheitswürfeln. Es gibt je einen, der aus 2, 3, 4, 5, 6 bzw. 7 Einheitswürfeln zusammengesetzt ist.
Für die beiden Exhibits gibt es aus der ursprünglichen HdMa on tour Variante natürlich wieder je eine Anleitungskarte mit Forschungsauftrag.
Gemäß des im Abschnitt vorher genannten Bedürfnisses, die HdMa on tour auch Kindern mit mangelnden sprachlichen Kenntnissen oder mit Leseschwierigkeiten einen eigenständigen Zugang zum Exhibit zu ermöglichen, entwickelten wir auch für die Würfel-Exhibits Anleitungskarten ohne Text.
Analog zu vorher liegt es an der Organisation des Lehr/Lernsettings die Forschungsaufträge in verbaler Form den Kindern zugänglich zu machen.
 Abb. 7 Anleitungskarte T-Würfel |
|
|
|
|
|
Für die Würfel-Exhibits gibt es ebenfalls einen Holzrahmen als Orientierungshilfe, umgesetzt in Form einer Holzplatte, die eine quadratische Ausnehmung hat, in die die Grundfläche des zu bauenden Würfels perfekt passt. Speziell für lernschwache Schülerinnen und Schüler ist es oft nicht selbstverständlich, dass ein Würfel eine quadratische Grundfläche hat. Dieser Zusammenhang wird durch diese Orientierungshilfe so unterschwellig erfahrbar gemacht.
Einzig für den „T-Würfel“ gibt es so wie im vorhergehenden Abschnitt ein Einlageblatt, das die Anordnung der Teile in der untersten Ebene des zu bauenden Würfels vorgibt. Weil man aber aufgrund der Anordnung in der untersten Ebene noch lange nicht die räumliche Anordnung der einzelnen Bauteile für alle Würfelarten abbilden kann, mussten wir zu einer weiteren Art der gestuften Hilfe greifen:
Wir entwickelten jeweils für eine Lösungsmöglichkeit jedes Würfels eine Schritt für Schritt Anleitung. Das Design für diese Schritt für Schritt Anleitung ist in Form eines Leporellos ausgeführt: Dies ist ein Faltbuch, das ziehharmonikaartig zusammengelegt ist, siehe Abb. 11. Junker (1999) zeigte in ihrer Studie, dass das „richtige“ Sehen und das Einnehmen verschiedener Perspektiven Probleme bereiten kann. Um Hilfestellung bezüglich einer Facette der räumlichen Orientierung zu geben, kann man die Schritt für Schritt Anleitung, da sie eben in dieser speziellen Leporelloform ausgeführt ist, auch in aufrechter Positionierung hinstellen und unterstützt Kinder dabei im Wahrnehmungsprozess.
|
|
Abb. 11 Leporello „Natürliche Zahlen Würfel“ |
|
Auf den ersten Blick erscheint die Schritt für Schritt Anleitung für den T-Würfel vom Aufbau her mit dem des natürliche Zahlen Würfels ident zu sein: Im oberen Bildfeld jeder Seite des Leporellos wird immer das Bauteil dargestellt, das in den zu bauenden Würfel im nächsten Schritt eingefügt werden muss. Im zu bauenden Würfel wird es dem Arbeitsschritt entsprechend farblich hervorgehoben. Allerdings unterscheiden sich die zwei Anleitungen in einem vermeintlich marginalen Unterschied: Beim „T-Würfel“ werden die T – förmigen Bauteile im oberen Bildfeld jeder Seite immer in derselben räumlichen Lage dargestellt, so dass die gemeinsame T – förmige Struktur gut erkennbar ist. Durch diese Darstellung muss aber für jedes T – förmige Teil beim Einbauen in den Würfel eine gedankliche räumliche Drehung vorgenommen werden.
Beim Natürliche Zahlen Würfel versuchten wir in der Darstellung der zu verwendenden Bauteile die später notwendige räumliche Orientierung schon vorweg zu nehmen. Das heißt, die Würfel wurden im oberen Feld der Anleitungsseite so positioniert, wie sie in den Würfel dann eingefügt werden müssen. Allerdings eröffnet sich hier die Schwierigkeit, dass es in der Abbildung „verdeckte“ Einheitswürfel gibt. Das Erfassen dieser unsichtbaren Würfel, bzw. die nicht vordergründlich gut wahrnehmbaren Leerräume stellen bestimmt eine große Herausforderung für manche Kinder dar.
Die Station „Dudeney’s Zerschneidung“ ist das sogenannte Haberdasher’s Puzzle. Es besteht aus einem Dreieck und drei Vierecken, die man einerseits zu einem Dreieck andererseits aber auch zu einem Quadrat zusammenfügen kann.
Die hier beschriebenen, vorhergehenden Stationen erfordern von den Kindern die Strategieentwicklung, um bestimmte Legearten herauszufinden. Diese Hürde wollten wir im Neudesign der Station „Dudeney’s Zerschneidung“ umgehen, damit ein anderer Aspekt der Auseinandersetzung mit dem Exhibit stattfinden kann. Wir greifen dabei auf eine Idee von Dudeney zurück, die er in seinem Buch „Canterburry Puzzels“ schildert:
“I add an illustration showing the puzzle in a rather curious practical form, as it was made in polished mahogany with brass hinges for use by certain audiences. It will be seen that the four pieces form a sort of chain, and that when they are closed up in one direction they form the triangle, and when closed in the other direction they form the square.” (Dudeney 1919, S. 180)
Die vier Teile des Puzzles sind in unserer Ausführung mit Hilfe von Scharnieren an einander gefügt. Je nachdem wie man die Teile aneinander klappt, entsteht ein gleichseitiges Dreieck oder ein Quadrat. Da die beiden Figuren durch Zusammensetzen aus denselben vier verschiedenen Teilen entstehen, kann hier der Fokus auf das Erfahrungssammeln im Bereich Flächeninhaltsgleichheit durch Zerlegungsgleichheit gelegt werden. (Abb. 12)
Auch zu diesem Exhibit wurden Anleitungskärtchen mit und ohne Text entwickelt, analog zu den bereits hier beschriebenen Formaten. Weitere Differenzierungsstufen sind hier nicht angedacht, da durch die Ausfertigung des Puzzles mit den Scharnieren nur die zwei gewünschten Figuren gelegt bzw. geklappt werden können.
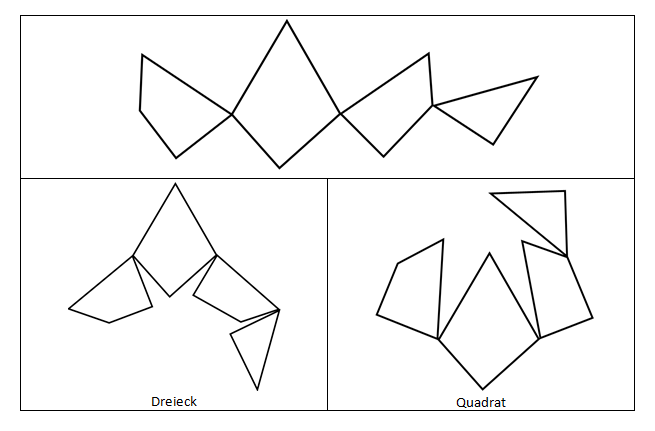
Abb. 12 Exhibit „Dudeney’s Zerschneidung“
Das Nim-Spiel gehört zu den mathematischen Spielen, die Kinder zum Entdecken und Erforschen von Spielstrategien herausfordern. Die Ausgangssituation ist, dass sich in allen Vertiefungen des Spielfeldes Spielsteine befinden. Zwei Kinder spielen gegeneinander. Es werden abwechselnd die Spielsteine vom Spielfeld entfernt. Es dürfen in einem Zug 1, 2 oder 3 Spielsteine aus einer Reihe entfernt werden. Voraussetzung für das Spiel ist lediglich, dass die Kinder bis 3 zählen können, aber sie werden im Verlauf des Spiels rasch Entdeckungen machen, dass das Nim-Spiel kein Glücksspiel ist. Es gilt bestimmte Anzahlen, die auf dem Spielfeld in einem Zug verbleiben sollen, zu erreichen, sodass man sicher gewinnen kann.
Um Kindern mit mangelnden Deutschkenntnissen oder Leseschwierigkeiten die Grundregeln dieses Spiels zu vermitteln, haben wir versucht, die Anleitungskarte ohne Text wieder piktographisch zu übersetzen, siehe Abb. 15.
Vielleicht erfinden die Schülerinnen und Schüler mit dieser Grundinformation selbst Regeln, entwickeln Möglichkeiten einen Sieger bzw. eine Siegerin zu ermitteln. Es geht primär darum, aus den Aktionen, die man selbst beziehungsweise der andere setzt, Schlüsse zu ziehen, damit man als Gewinner, als Gewinnerin hervorgeht.
|
|
|
Um weiter zu differenzieren, kann man natürlich für die Kinder das Spielfeld einschränken und z.B. nur die letzte Reihe des Spielfelds verwenden. Aus dieser Reihe dürfen in einem Zug entweder 1 oder 2 Spielsteine entfernt werden. Auch in dieser Version gibt es ein reichhaltiges Angebot an mathematischen Entdeckungen, bestimmte „gewinnbringende“ Anzahlen müssen vom Kind einerseits gemerkt werden, aber auch immer wieder angestrebt werden, sie zu erreichen. Diese Anzahlen zu erreichen, bedeutet für das Kind ein Operieren im Kopf, Handlungen müssen abgewogen werden, Konsequenzen überlegt, also eine Strategie entwickelt werden.
Lernschwache Schülerinnen und Schüler brauchen, um solche Strategien entwickeln zu können, häufig die Begleitung durch eine Lehrperson oder einer Mitschülerin oder einen Mitschüler.
Die HdMa on tour ist organisatorisch so angelegt, dass die 30 Stationen für ein bis zwei Wochen an einem Standort verbleiben können. Dadurch ergeben sich unterschiedliche Einsatzmöglichkeiten:
Wie empfehlen einen „Erlebnisraum“ zu gestalten (vorzubereiten): Ein eigener Raum wird gestaltet, in den die Kinder für ein bestimmtes Zeitfenster zum Arbeiten mit den Exhibts der HdMa on tour kommen. Die vorbereitete Umgebung lädt sofort zum Tun ein. Maria Montessori hat den Ausdruck der vorbereiteten Umgebung geprägt:
„Die Grundlage ist also nicht das Nachdenken darüber, wie man das Kind lehren oder erzieherisch beeinflussen kann, sondern wie man ihm eine Umgebung schaffen kann, die seiner Entwicklung förderlich ist, um es dann in dieser Umgebung sich frei entwickeln zu lassen.“ (Montessori 2014, S. 50)
Der Besuch in diesem Erlebnisraum kann ein einziges Ereignis sein oder mehrmals pro Woche stattfinden. Zur Kennzeichnung dieses Raumes wird ein Roll-Up aufgestellt, das Bestandteil der HdMa on tour ist. Der Lehrkraft obliegt die Entscheidung, welche Aufträge die Kinder erfüllen sollen: Wieder lässt sich hier der Bogen spannen von einem freien Lernsetting (die Kinder beschäftigen sich mit dem Material) bis zu einem instruierten Lernsetting. Die Stufen der Anforderung kann man auch durch flexible Hilfe erzeugen, d.h. nicht von vornherein sind allen Schülerinnen und Schülern die Rahmen bzw. Einlageblätter zugänglich, sondern sie werden bei Bedarf gegeben.
Die Kinder arbeiten mit den Exhibits gemäß ihrer individuellen Potenziale (Entwicklungsbereiche wie etwa Motorik/Wahrnehmung, Denken/Lernstrategien, Kommunikation/Sprache, Emotionen/soziales Handeln) und erweitern dabei ihre Kompetenzen (Wissen, Können, Haltung, Motivation).
Die Erfahrung aus der Arbeit der Lehrerinnen und Lehrer mit derzeit 10 199 Schülerinnen und Schülern in Österreich (Stand 15.1.2017) zeigt, dass die Sozialform in der Erarbeitung der Kinder mit den Exhibits der HdMa on tour nicht der entscheidende Faktor für den Tiefengrad in der Auseinandersetzung mit den mathematischen Problemstellungen ist. Dies war aufgrund der Gespräche mit den Lehrern und Lehrerinnen bei der Rückgabe der Materialien ersichtlich. Jedoch zeigt sich durch die Erfahrung der Lehrerinnen und Lehrer, dass die Initiierung von sogenannten „ICH-DU-WIR Phasen“ zu guten Ergebnissen geführt hat: Die Kinder waren zuerst aufgefordert in einer ICH-Phase alleine mit einem Exhibit entdeckend zu arbeiten, außer bei den partnerschaftlichen Strategiespielen. Es folgte die DU-Phase mit einem anderen Kind, in der über erste Lösungsansätze und Entdeckungen zum Exhibit mit einem Lernpartner, einer Lernpartnerin diskutiert wurde. In einer WIR-Phase konnten mehrere Kinder und/oder der Lehrer, die Lehrerin mit einer Gruppe Vermutungen aufstellen, Ergebnisse vergleichen und prüfen. Die Kommunikation im inklusiven Mathematikunterricht erreichte hier einen großen Stellenwert.
Der methodische Zugang, wie Lehrerinnen und Lehrer, die gestuften Hilfen einsetzen können, lässt mehrere Varianten zu. Die Lehrerinnen und Lehrer haben die Möglichkeit aus diesem nun breiten Spektrum an Differenzierungsmöglichkeiten ein Lernarrangement individuell angepasst für ihre Lerngruppe bzw. für einzelne Schülerinnen und Schüler zusammenzustellen. Ein methodischer Zugang, der auch dem Aspekt der natürlichen Differenzierung, also vom Kind aus, entspricht, wäre folgender: Die Lehrerinnen und Lehrer zeigen den Schülerinnen und Schülern exemplarisch mit einem Exhibit alle Differenzierungsmöglichkeiten, Anleitungskarte mit Text und ohne Text, den Holzrahmen, die Einlage für den Holzrahmen und besprechen den Zugriff auf diese Hilfestellungen. Bei jedem einzelnen Exhibit kann der Schüler, die Schülerin eigenständig entscheiden, auf welche Hilfen er/sie zurückgreift. Dies kann von Exhibit zu Exhibit variieren und ist nicht vorher festlegbar. Werden die Schülerinnen und Schüler mit den mathematischen Problemstellungen vertrauter, verlangen sie möglicherweise bei weiteren Exhibits nach weniger Hilfestellungen. Lösen sie ein Exhibit mit einer Hilfestellung, z.B. dem Holzrahmen mit Einlage, versuchen sie vielleicht dasselbe Exhibit ein zweites Mal ohne den Holzrahmen und ohne Einlage zu lösen, was durchaus komplexer in der Anforderung ist. An dieser Stelle sind reflexive Denkprozesse von mehreren Erarbeitungsdurchgängen vorstellbar, die zu erweiterten Entdeckungsprozessen führen können.
Die PH- Wien bietet eine Fortbildungsveranstaltung „Haus der Mathematik on tour“ an. In dieser Veranstaltung lernen die Teilnehmerinnen und Teilnehmer das Konzept von HdMa on tour kennen. Sie bekommen einen Einblick in forschendes und entdeckendes Lernen im Mathematikunterricht. Die Teilnehmerinnen und Teilnehmer haben die Möglichkeit sich mit den Exhibits eigenständig auseinander zu setzen und wie ihre Schülerinnen und Schüler vom An-greifen zum Be-greifen zu gelangen. Schließlich werden anhand von ausgewählten Beispielen die Möglichkeiten des differenzierten Arbeitens mit der HdMa on tour aufgezeigt.
Ziel ist es, dass die HdMa on tour differenziert alle Lernenden unterstützt, mit ihren unterschiedlichen Lernvoraussetzungen bestmöglich im Entdeckungsprozess umzugehen, mathematische Einsichten zu erwerben, dadurch Vertrauen in die eigenen Leistungen und damit verbunden auch Freude am mathematischen Lernen zu entwickeln.
Die differenzierten Lernzugänge mit den Exhibits der HdMa on tour gilt es nun zu erproben und wissenschaftlich zu evaluieren. Auf Grund der zukünftigen Evaluierungen, können einerseits weitere Lernzugänge für die bestehenden Exhibits konzipiert werden und andererseits die gewonnen Erkenntnisse beim Erstellen neuer Exhibits im Designprozess bereits mitgedachte werden.
Cope, Liza (2015): Math Manipulatives: Making the Abstract Tangible. In: Delta Journal of Education 5 (1), S. 10–19.
Crowley, Mary L. (1987): The van Hiele Model of the Development of Geometric Thought. In: Mary Montgomery Lindquist (Hg.): Learning and teaching geometry, K-12. 3. print. Reston, Va.: National Council of Teachers of Mathematics (Yearbook/National Council of Teachers of Mathematics), S. 1–16.
Devlin, Keith J.; Diener, Immo (2002): Muster der Mathematik. Ordnungsgesetze des Geistes und der Natur. 2. Aufl. Heidelberg: Spektrum Akad. Verl.
Dudeney, Henry Ernest (1919): Canterbury puzzles, and other curious problems. 2. Aufl. London: Thomas Nelson and Sons, LTD. Online verfügbar unter http://www.gutenberg.org/files/27635/27635-h/27635-h.htm.
Häsel-Weide (2015): Gemeinsames Mathematiklernen - im Spiegel von Inklusion. In: Rita Braches-Chyrek, Carina Fischer, Cosimo Mangione, Anke Penczek und Sibylle Rahm (Hg.): Herausforderung Inklusion. Schule - Unterricht - Profession, Bd. 5. Bamberg: University of Bamberg Press (Forum Erziehungswissenschaft und Bildungspraxis, Band 5), S. 191–200.
Heimlich, Ulrich; Wember, Franz B. (Hg.) (2012): Didaktik des Unterrichts im Förderschwerpunkt Lernen. Ein Handbuch für Studium und Praxis. 2., aktualisierte Aufl. Stuttgart: Kohlhammer (Heil- und Sonderpädagogik).
Hengartner, Elmar; Hirt, Ueli; Wälti, Beat (2010): Lernumgebungen für Rechenschwache bis Hochbegabte. Natürliche Differenzierung im Mathematikunterricht. 2. aktualisierte und erweiterte Auflage. Zug: Klett und Balmer Verlag (Spektrum Schule - Beiträge zur Unterrichtspraxis).
Hußmann, Stefan; Prediger, Susanne (2007): Mit Unterschieden rechnen – Differenzieren und Individualisieren. In: Praxis der Mathematik in der Schule 49 (17), S. 1–8.
Junker, Barbar (1999): Räumliches Denken bei lernbeeinträchtigten Schülern. In: Die Grundschulzeitschrift 13 (121), S. 22–24.
Lederman, Susan J.; Klatzky, Roberta L. (1987): Hand movements: A window into haptic object recognition. In: Cognitive psychology 19 (3), S. 342–368.
McLean, Kathleen (1996): Planning for people in museum exhibitions. Washington, DC: Association of Science-Technology Centers.
Montessori, Maria (2014): Grundlagen meiner Pädagogik. Und weitere Aufsätze zur Anthropologie und Didaktik. 12., unveränderte Auflage, ungek. Ausg. Wiebelsheim: Quelle & Meyer.
Rosli, Roslinda; Goldsby, Dianne; Capraro, Mary Margaret (2015): Using Manipulatives in Solving and Posing Mathematical Problems. In: CE 06 (16), S. 1718–1725. DOI: 10.4236/ce.2015.616173.
Scherer, Petra; Moser Opitz, Elisabeth Moser (2010): Fördern im Mathematikunterricht der Primarstufe. Heidelberg: Spektrum Akademischer Verlag (Mathematik Primar- und Sekundarstufe). Online verfügbar unter http://site.ebrary.com/lib/alltitles/docDetail.action?docID=10394543.
Siew, Nyet Moi; Chong, Chin Lu; ABdullah, Mohamad Razali (2013): Facilitating students geometric thinking through van Hiele's phase-based learning using tangram. In: Journal of Social Sciences 9 (3), S. 101–111. DOI: 10.3844/jssp.2013.101.111.
Swan, Paul; Marshall, Linda (2010): Revisiting Mathematics: manipulative materials. In: Australian Primary Mathematics Classroom 15 (2), S. 13–19. Online verfügbar unter http://files.eric.ed.gov/fulltext/EJ891801.pdf.
Wember, Franz B. (2005): Mathematik unterrichten - eine subsidiäre Aktivität? Nicht nur bei Kindern mit Lernschwierigkeiten! In: Petra Scherer (Hg.): Fördern durch Fordern. Zwanzigerraum. 2 Bände. Horneburg: Persen (Produktives Lernen für Kinder mit Lernschwächen, Fördern durch Fordern / von Petra Scherer. Ill.: Ines Rarisch ; Bd. 1), S. 270–287.
Wittmann, Erich Christian (2010): Natürliche Differenzierung im Mathematikunterricht der Grundschule – vom Fach aus. In: Petra Hanke (Hg.): Anspruchsvolles Fördern in der Grundschule. Münster: ZfL-Verl. (Zfl-Text, 26), S. 63–78.