Abstract: Im Artikel werden Forschungsergebnisse aus zwei Projekten vorgestellt und mit Hilfe von komparativen Analysen verglichen. Hierzu werden zwei theoretische Grundpfeiler aufgebaut. Der erste fokussiert auf den wechselseitigen Bezug von mathematischem und sprachlichem Lernen, der zweite prägt ein Verständnis von Lernen als einen über die Institutionen verlaufenden Prozess, wonach sich Bildung am Kind und nicht an den Institutionen orientiert. Die Ergebnisse beider Projekte münden in einer gemeinsamen Rekonstruktion von sprachlichen Bedingungen des Mathematiklernens und sollen eine Basis für die noch zu erbringende Entwicklung ganzheitlicher Förder- und Fortbildungskonzeptionen für Kinder, Erziehende und Lehrpersonen schaffen.
Stichworte: Grundschulmathematikdidaktik; Sprache und Mathematik; inklusives Mathematiklernen; frühe mathematische Bildung; Interpretative Unterrichtsforschung
Inhaltsverzeichnis
Ausgangspunkt der folgenden Betrachtung von mathematischen Lernprozessen stellen Ergebnisse internationaler Vergleichsstudien dar, wie z. B. PISA, die einhellig zu folgendem Schluss kommen: Das deutsche Schulsystem erbringt durch früh einsetzende Selektionsprinzipien keine hohe Qualität an Schulleistungen in seiner Breite, sondern hebt die Chancenungleichheit innerhalb des Systems Schule auf ein internationales Spitzenniveau. Acht von elf Ländern mit der höchsten Chancengleichheit unter den OECD-Staaten schaffen es hingegen, bei Schülerinnen und Schülern beispielsweise eine hohe Qualität an Lesekompetenz zu erreichen (vgl. OECD 2005). Der Erfolgsschlüssel zur Etablierung von Schulsystemen mit international vergleichbarer hoher Qualität scheint demnach nicht in einer frühzeitigen Auslese, sondern in der gezielten Integration einer vielfältigen Schülerschaft zu liegen. Die einfache Formel könnte lauten: Chancengleichheit schafft Qualität in der Breite. Hierzu ist ein konstruktiver Umgang mit sprachlich-kultureller Vielfalt erforderlich. Dies gelingt in deutschen Schulen anscheinend bis jetzt höchstens ansatzweise (vgl. Schütte & Kaiser 2011).
Aufgrund dauernder Zuwanderung hat mittlerweile nahezu ein Drittel aller Schülerinnen und Schüler in deutschen Schulen einen Migrationshintergrund. In Großstädten wird dieser Anteil vielerorts deutlich übertroffen. Werden die Bedingungen des Unterrichts in naher Zukunft nicht an die bestehenden Verhältnisse sprachlich-kultureller Pluralität angepasst, wird ein großer Teil der in Deutschland zur Schule gehenden Kinder kaum erfolgreich am Bildungssystem teilhaben können, wodurch der Erfolg des gesamten Schulsystems gefährdet wäre (vgl. OECD 2006).
Infolge des Normierungsansatzes der Schule an den Fähigkeiten ‚der deutschen Schüler_in’ und einem diesbezüglich zugrundeliegenden Verständnis von Monolingualität als Normalzustand von Kindern in der deutschen Schule (vgl. zum monolingualen Habitus der deutschen Schule Gogolin 1994, S. 30 ff.; vgl. auch Schütte 2009) verwundert es kaum, dass eine Veränderung dieser Situation nach einhelliger Meinung meist mit dem Überkommen ‚unterrichtssprachlicher’ Defizite von Kindern verbunden wird. Es erscheint hierbei fraglos, dass im Beherrschen der Unterrichtssprache Deutsch ein Schlüssel für Schulerfolg liegt. Das Beherrschen der Unterrichtssprache hat dabei fraglos aus vielerlei Gründen auch und gerade maßgeblichen Einfluss auf die Leistungen im Fachunterricht, auch im Fach Mathematik (vgl. Deutsches PISA-Konsortium 2004 Heinze & Rudolph-Albert 2008; Schütte 2009, Schütte & Kaiser 2011). Diese monokausale Betrachtung lässt jedoch außer Acht, wie einer vielfältigen Schülerschaft mit innovativen Lehr- und Unterrichtskonzepten der Zugang zu Bildung erleichtert werden könnte, die nicht vorab die Fähigkeiten im Deutschen als begrenzenden Zugangsschlüssel wählt. Großes Potential zur Veränderung der Situation steckt hiernach in Ansätzen, welche auch den Fachunterricht als Ort des Sprachlernens ansehen (vgl. Riebling 2013)
So werden in der internationalen mathematikdidaktischen Diskussion in jüngerer Zeit Ansätze vertreten, die der Sprache und der kommunikativen Kompetenz für das Lernen mathematischer Inhalte eine besondere Bedeutung zuweisen (vgl. u. a. Pimm 1987; Zevenbergen 2001). Moschkovich (2002, 196) betont hierüber hinaus das Diskursive des Mathematiklernens. Mit ihrer „situated-sociocultural“ Perspektive auf Mathematiklernen ist ein Paradigmenwechsel verbunden von einer Betrachtung von Defiziten der Lernenden hin zu Ressourcen und Kompetenzen einer vielfältigen Schülerschaft. Nach dieser Perspektive findet Mathematiklernen in einem sozialen Kontext statt, in den die Beteiligten unterschiedliche Sichtweisen der Situation einbringen und interaktiv aushandeln. (vgl. ebd.). Verstärkt wird dieser Zusammenhang dadurch, dass, auch aufgrund der Einführung der Bildungsstandards, in deutschen Schulen der sprachlichen Aushandlung im Mathematikunterricht eine immer größere Bedeutung zukommt. So wird im Mathematikunterricht mittlerweile von Schülerinnen und Schülern erwartet, dass sie prozessbezogene Kompetenzen erlangen sollen, wie kommunizieren, argumentieren, darstellen, modellieren oder problemlösen (vgl. KMK 2004). Diese zunehmende Bedeutung der Sprache beim Lernen im Fach auch in frühen Lernprozessen führt zu einer Betrachtung von Lernprozessen, die über den Lernort Schule hinausweist.
Untersucht man die mathematische Entwicklung von Kindern, so ist es nach Fthenakis et al. (2009) vor allem auch notwendig, die unterschiedlichen Lernorte des Kindes einzubeziehen. Hierzu zählen vor allem die Kita und die Familie. In Bezug auf Mathematiklernen in der Familie lassen sich jüngst Studien in der deutschsprachigen Mathematikdidaktik finden, wie z. B. die Arbeit von Tiedemann (2012). Betrachtet man das institutionalisierte Lernen von Kindern vor der Schule, so ist in den letzten Jahren vordergründig die sprachliche Bildung ins Zentrum der Betrachtung gerückt und – erst etwas zeitverzögert – die mathematische Bildung. So wurden in den letzten Jahren, beginnend mit dem Schuljahr 2002/2003 (vgl. Voet Camelli 2008) in allen deutschen Bundesländern vielfältige Versuche unternommen, vor allem die sprachlichen Defizite von Kindern vor Schuleintritt zu diagnostizieren und auszugleichen, um so positiven Einfluss auf ein späteres fachbezogenes Lernen in der Grundschule zu nehmen. Dies jedoch ohne zuvor zu ergründen, welche vorhandenen sprachlichen Fähigkeiten genutzt werden könnten, um fachliches Lernen jenseits der bestehenden Normen erfolgreich zu gestalten. Eine solche Perspektive auf die Kompetenzen von Kindern vor Schuleintritt folgt der oben beschriebenen monolingualen Orientierung.
Die Ergebnisse zum Leistungsvergleich von deutschen Grundschülern des IQB (vgl. Stanat et al. 2012) offenbaren allerdings, dass die Bemühungen der frühkindlichen Sprachförderung der letzten Jahre nicht die gewünschten Erfolge für das spätere fachliche Lernen in der Grundschule erzielen. Sprachförderkonzepte, die neben allgemeinen sprachlichen Kompetenzen einen interdisziplinären Blick über das Fach Deutsch hinweg in andere Fächer zulassen und so auch positive Effekte im fachbezogenen Lernen der Schule erzielen könnten, scheint es zudem kaum zu geben. Untersuchungen der erziehungswissenschaftlichen Migrationsforschung (vgl. Gogolin 2006) ebenso wie aktuelle Untersuchungen der mathematikdidaktischen Forschung (vgl. z. B. Heinze et al. 2011, Schütte & Kaiser 2011, Schütte 2010) kommen jedoch einhellig zu dem Schluss, dass nicht die Beherrschung von allgemeinen sprachlichen Kompetenzen für das erfolgreiche Lernen im Fach (Mathematik) bedeutsam ist, sondern der Erwerb von Kompetenzen in einer fachbezogenen Bildungssprache. Insofern scheinen Forschungsprogramme zu fehlen, die erst einmal die Grundlage für eine gezielte Förderung schaffen. In diesem Zusammenhang ist – bezogen auf das deutsche Schulsystem – kritisch anzumerken, dass es keine umfassenden Programme oder didaktischen Umsetzungen gibt, welche die sprachlichen Fähigkeiten, die Zweitsprachlernende mitbringen, gebührend im Schulunterricht würdigen (vgl. Gogolin 1994 sowie Schütte 2009). Einzelne Schulversuche, die bilingualen Unterricht anbieten oder aber mit begrenzten Unterrichtsversuchen an einer „lebensweltlichen Mehrsprachigkeit“ (Gogolin 1994) von Kindern anknüpfen, seien hiervon ausgenommen (vgl. Meyer & Prediger 2011).
Im Weiteren werden Ergebnisse dargestellt, die strukturelle Gemeinsamkeiten bei der sprachlichen Gestaltung von mathematischen Lernprozessen aufzeigen, die über die Lernorte KiTa und Schule sowie über das jeweilige Alter der Kinder hinwegweisen. Sie geben Grund zu der Hypothese, dass ein Schlüssel zu einer besseren Förderung von Kindern im Bereich des sprachbezogenen fachlichen Lernens – vor allem im Bereich der Mathematik – primär in der optimaleren Aus- und Fortbildung der pädagogischen Fachkräfte liegen sollte, was erst sekundär zu einer Verbesserung von ‚sprachlichen’ Kompetenzen der Kinder führen wird. Eine Verkürzung des Problems auf die Verbesserung von nicht der ‚Norm’ entsprechenden sprachlichen Kompetenzen bei Kindern würde hiernach zu kurz greifen und das Bild defizitärer Kinder bekräftigen.
Im folgenden Kapitel werden die theoretischen Grundlagen hergeleitet, auf deren Basis Mathematiklernen in der KiTa und der Grundschule aus sprachlicher Perspektive analysiert wird. Hieran anschließend werden in Kapitel drei die beide Projekte betreffenden, methodischen Festlegungen dargestellt. Im Kapitel vier werden Analyseergebnisse aus beiden Projekten vorgestellt. Im fünften Abschnitt wird der theoretische Zugewinn mit Hinweisen für die Ausbildungen von pädagogischen Fachkräften sowie für die Gestaltung von Lernprozessen für Kinder dargestellt.
Zur Analyse sprachbezogenen fachlichen Lernens von Mathematik lässt sich auf Ausführungen von Pimm (1987) zurückgreifen. Pimm vergleicht die Lehrperson als einen „native speaker“ (S. 2) der Mathematik mit Schülerinnen und Schülern, für die Mathematik unverständlich zu sein scheint, wie eine Fremdsprache, derer sie nicht mächtig sind. In diesem Zusammenhang greift Pimm (1987) auf den Registeransatz von Halliday zurück. Nach Halliday (1975) lässt sich ein Register als eine Menge von Bedeutungen verstehen, die innerhalb einer (fach)spezifischen Situation, in der Sprache Anwendung findet, geeignet sind, zusammen mit den Wörtern und Strukturen, die diese Bedeutungen ausdrücken (z. B. Gespräch zwischen Arzt und Patient, Mathematikunterricht. In diesem Sinne ist die Entwicklung eines Registers mehr als der Prozess, neue Wörter zu einer Terminologie hinzuzufügen (vgl. ebd.). Pimm (1987) sieht die Aufgabe von Lernenden darin, ein mathematisches Register sprachlich zunehmend zu beherrschen und so perspektivisch in und mit diesem verbal handeln zu können, wie ein native speaker der Mathematik. Bezogen auf diesen theoretischen Ansatz lässt sich demnach der Frage nachgehen, wie Lernende in Aushandlungsprozessen beim Lernen von Mathematik von Betreuenden unterstützt werden können, neben mathematischen Entdeckungen ein mathematisch-fachsprachliches Register aufzubauen (vgl. auch Schütte 2009 und 2010).
Nicht auf ein fachbezogenes Registers begrenzt, jedoch weiterhin den Blick eher auf Defizite von Kindern gewandt, lässt sich sprachbezogenes mathematisches Lernen auf mathematische Ansätze Bezug nehmen, die in Anlehnung an theoretische Ausführungen von Gogolin (2006) und Cummins (2000) zu verstehen sind. Nach Gogolin (2006) wird in der deutschen Schule an alle Schülerinnen und Schüler der normative Anspruch herangetragen, dass diese die im Unterricht gepflegten Sprachvarianten der Schule beherrschen. Dieses Konzept der „Bildungssprache“ (ebd., S. 82 ff.) lehnt Gogolin an ein von Cummins (2000, S. 57 ff.) beschriebenes Konzept der „Cognitive Academic Language Proficiency“ an. Cummins trennt „academic language proficiency“ von „conversational language proficiency“, womit er darauf verweist, dass Kinder in ihrer Zweitsprache schnell Fähigkeiten erwerben, die sie in Alltagssituationen anwenden können. Bedeutend länger benötigen sie, um Kompetenzen in der Bildungssprache des Unterrichts zu erlangen. Ein entscheidendes Charakteristikum der Bildungssprache stellt ihre konzeptionelle Schriftförmigkeit dar, wodurch sie ein hohes Maß an Informationsdichte sowie eine Situationsentbundenheit aufweist und in wesentlichen Merkmalen nicht der mündlichen Kommunikation des Alltags vieler Schülerinnen und Schüler entspricht. Empirische Untersuchungen im deutschsprachigen Raum, die eine Bildungssprache des Unterrichts genauer charakterisieren könnten, liegen bislang kaum vor. Ansätze die sich damit beschäftigen, stellen meist Programme da, die auf der normativen Festlegung dessen, dass das Beherrschen einer Bildungssprache wichtig wäre, Ansätze entwickeln, wie diese zu fördern sei. Gogolin und Roth (2007) geben zumindest Teilbereiche an, die für das Beherrschen einer Bildungssprache relevant sein könnten. Hierzu zählen das Passiv, unpersönliche Ausdrücke, der Konjunktiv, Konstruktionen mit lassen, Substantivierungen, Komposita und Attribute.
Andere Ansätze vor allem aus der internationalen mathematikdidaktischen Forschung kritisieren diese Begrenzung der Betrachtung von Mathematiklernen aus sprachlicher Perspektive. Moschkovich (2002, 196) betont die „situated-sociocultural“ Perspektive auf Mathematiklernen und grenzt sich von Ansätzen, die Mathematiklernen als „constructing multiple meanings of words“ (Moschkovich 2002, S. 193) verstehen und sich so meist auf den Registerbegriff von Halliday (1975) beziehen, ab. Solche Ansätze fokussieren nach Moschkovich vor allem auf Differenzen zwischen den Fähigkeiten von Kindern, in oder mit unterschiedlichen Registern sprachlich zu handeln. Diese defizitorientierte Betrachtung erhebt ein Register zum Ziel sprachlichen/mathematischen Handelns, dessen Beherrschung als hinreichend für Schulerfolg und mathematisches Verständnis betrachtet wird. Andere sprachliche Fähigkeiten aus alltäglichen Erfahrungsräumen von höchst unterschiedlichen Kindern wären hiernach weniger bedeutsam und würden im Mathematik- oder Fachunterricht keine Aufmerksamkeit erhalten. Mit der „situated-sociocultural“ Perspektive vollzieht sich nach Moschkovich ein Wechsel von der Betrachtung von Hindernissen und Defiziten der Lernenden hin zu Ressourcen und Kompetenzen einer vielfältigen Schülerschaft. Hiernach findet Mathematiklernen stets in einem öffentlichen sozialen und kulturellen Kontext statt und stellt eine diskursive Tätigkeit dar. Bei diesem Bild von Mathematiklernen gibt es nicht den einen richtigen, zu erreichenden mathematischen Diskurs. Alle Lernenden partizipieren diesem Gedankengang folgend an mathematischen Diskursen in unterschiedlichen communities und gebrauchen hierfür vielfältige Ressourcen aus unterschiedlichen Registern, um mathematisch erfolgreich zu kommunizieren (vgl. Gee 1999; Moschkovich 2002).
„Allthough register may be an inherently social concept, Gee’s definition of Discourse reminds (and perhaps forces) us to include more than words and meanings ...and that aspects other than language, such as interactional and nonlanguage symbol systems, should be included in discours analysis“ (Moschkovich, S. 199)
Der Begriff mathematical Discourse macht deutlich, dass bei dieser Betrachtung des Lernens von Mathematik interaktionale oder nonverbale Aspekte (vgl. Huth 2011)im Gegensatz zu Registeransätzen einen zentralen Stellenwert des Verständnisses von Mathematiklernen einnehmen. In diesem Zusammenhang sei auch auf das diagrammatische Argumentieren im Mathematikunterricht hingewiesen, welches zwar vielfältig über zeichnerische nonverbale Handlungen vollzogen werden kann, trotzdem nicht als ‚nichtsprachlich’, sondern als eine Form der sprachlichen Aushandlung und Begründung zu deuten sei (vgl. Krummheuer 2013; Schreiber 2010; Van Oers 1997).
In diesem Zusammenhang lässt sich auf vielfältige Arbeiten interaktionistischer Ansätze der Interpretativen Unterrichtsforschung der Mathematikdidaktik verweisen. So legt Krummheuer (1992) dar, dass Lernende beim Lernen von Mathematik in der Grundschule in „kollektive Argumentationen“ (ebd. S. 143) eingebunden werden. Erst durch die zunehmend autonomere Partizipation an diesen wird ihm folgend Mathematik gelernt (Krummheuer & Brandt 2001). In der Interaktion des Unterrichts deuten die Beteiligten das Geschehene aufgrund vielfältiger Fähigkeiten und Hintergründe höchst unterschiedlich. Im Zusammenhang mit der gegenseitigen Anpassung solch subjektiver Deutungen beim kollektiven Argumentieren spricht Krummheuer (1992, S. 22) von dem Begriff „Situationsdefinition“. Situationsdefinitionen werden ständig angeglichen und verändert. Dieses Hervorbringen veränderter Deutungen wird von Krummheuer (1992) dabei als eine entscheidende innerpsychische Voraussetzung für die kognitive Entwicklung des Individuums angesehen, da es eine Grundlage für die Konstruktion neuer Bedeutungen schafft und damit konstitutiv für Lernprozesse ist. Ziel sollte es sein, unter den Beteiligten eine als „[...] geteilt geltende Deutung“ (Krummheuer 1992, S. 34) zu erreichen, die meist nur einer geringen funktionalen Passung der individuellen Deutungen der Beteiligten bedarf. Auf der Basis dieser vorübergehender Bedeutungspassung, welche auch mit „Arbeitskonsensus“ (Krummheuer 1992, S. 25; zum Begriff „working consensus“ vgl. Goffman 1959, S. 9 f.) bezeichnet wird, kann sich die Interaktion erst weiterentwickeln. Die Hervorbringung von ‚einfachen’ Situationsdefinitionen wird jedoch nicht zwangsläufig zum Lernen von neuem führen. Standardisierte und routinisierte individuelle Situationsdefinitionen benennt Krummheuer (1992, S. 24 ff.) in Bezug auf Goffmans Begriff „frame“ (1974, S 19) als „Rahmung“. Die Rahmungen der Schülerinnen und Schüler untereinander sowie die der Lehrperson stimmen meist nicht überein (vgl. Krummheuer 1992) und müssen ebenfalls in der Unterrichtsinteraktion angeglichen und ausgehandelt werden. Unterricht lässt sich hiernach als eine „zur Praxis geronnene Schnittstelle von Rahmungen zweier unterschiedlicher Interaktionspraxen“ (ebd. S. 64) beschreiben. Die Lehrperson zieht zur Deutung fachlicher Aspekte des Unterrichts Rahmungen aus ihrer fachwissenschaftlichen und didaktischen Interaktionspraxis hinzu, die Schülerinnen und Schüler ziehen ihre Rahmungen aus ihrem außerschulischen Umfeld bzw. aus ihrer vorangegangenen Schullaufbahn. Erst die grundlegende Modifikation oder Konstruktion von Rahmungen stellt nach Krummheuer einen Lernprozess da (vgl. hierzu auch Schütte 2009).
„Mit dem Lernen neuer Rahmungen erschließt sich das Individuum einen neuen gesellschaftlichen Wirklichkeitsbereich. Es erwirbt eine neue Perspektive auf die Wirklichkeit,...“ (Krummheuer 1992, S. 45)
Hierzu müssen nach Krummheuer Rahmungsdifferenzen zwischen den Beteiligten, die das Hervorbringen von kollektiven Argumentationen erschweren, aber gleichzeitig den Motor des Lernens darstellen, zunehmend durch die in der fachlich geprägten Interaktion fortgeschrittene Person – also durch den Lehrenden, Erzieher_innen und Eltern – koordiniert werden.
Im Folgenden werden die Ergebnisse der Forschungsprojekte nacheinander dargestellt. Hierbei handelt es sich um ein Projekt, welches auf Kinder der Jahrgangsstufe 4 und ein anderes, welches auf Kinder von drei bis zehn Jahren fokussierte. Gemeinsam ist beiden Projekten, dass die beteiligten Kinder sowohl sprachlich als auch kulturell vielfältig waren.
In der ersten hier dargestellten Studie wird die sprachliche Gestaltung des Grundschulmathematikunterrichts durch die Lehrpersonen in Einführungsszenen neuer mathematischer Begriffe analysiert. In diesen Phasen kommt der sprachlichen Gestaltung des Unterrichts eine besondere Bedeutung zu, da es um den erstmaligen Aufbau von subjektiv neuem für die Schülerinnen und Schüler geht. Hierzu wurden drei Klassen der Jahrgangsstufe 4 zweier Hamburger Grundschulen mit einem Migrationsanteil von ca. 80 Prozent über vier Monate begleitet. Ziel der Untersuchung ist es, Gelegenheiten zum Lernen von Mathematik von Schülerinnen und Schülern in einem Grundschulmathematikunterricht theoretisch zu beschreiben, welcher durch sprachlich-kulturelle Pluralität der Schülerschaft geprägt ist. Nachfolgend werden ausgewählte Sequenzen einer Szene alltäglichen Grundschulmathematikunterrichts sowie deren zusammenfassende Analyse als illustrierendes Beispiel dargestellt.
Die Unterrichtsszene kgV[2]
Zu Beginn der Szene kgV befinden sich Frau Teichmann, die sowohl Mathematik- als auch Klassenlehrerin ist sowie neun Schülerinnen und 16 Schüler im Klassenraum, davon insgesamt 17 mit Migrationshintergrund. Der Großteil der Schülerinnen und Schüler stammt aus einem bildungsfernen familiären Umfeld mit vergleichsweise niedrigem sozioökonomischem Status. Frau Teichmann ist ausgebildete Gymnasiallehrerin. In der vorangegangenen Mathematikstunde wurde die Grundrechenart Multiplikation vertieft. In dieser Stunde soll die Einführung eines neuen mathematischen Begriffs stattfinden: das kgV – das kleinste gemeinsame Vielfache.

Nach der Berechnung von weiteren Vielfachen, zeichnet die Lehrperson zwei Kreise an die Tafel.

Es steht zu diesem Zeitpunkt somit folgende Zeichnung an der Tafel.
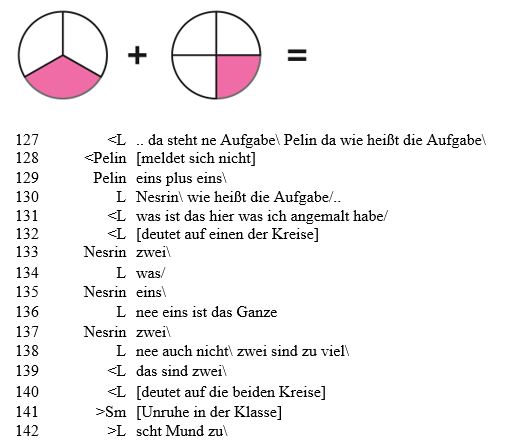
Im Anschluss hieran sagt Otto in <144> „ein Drittel“. Die Lehrperson paraphrasiert dies und schreibt ⅓ in das schraffierte Drittel des linken Kreises. Mehrere Kinder sagen „ein Viertel“ <152>. Die Lehrperson notiert dies in der Zeichnung und erweitert die Brüche ![]() und ¼ zu
und ¼ zu ![]() und
und ![]() . Etliche Schülerinnen und Schüler bringen phantasievolle Lösungen für deren Addition wie z. B.
. Etliche Schülerinnen und Schüler bringen phantasievolle Lösungen für deren Addition wie z. B. ![]() . Die Lehrperson geht auf diese Antworten nur insoweit ein, dass man dies nicht dürfe und addiert die Brüche zu
. Die Lehrperson geht auf diese Antworten nur insoweit ein, dass man dies nicht dürfe und addiert die Brüche zu ![]() . Abschließend folgt ihre Verallgemeinerung:
. Abschließend folgt ihre Verallgemeinerung:

Zusammenfassung der Analyse der sprachlichen Gestaltung – Szene mit dem Fokus auf den Zeilen <127-142>
Der Begriff „kleinstes gemeinsames Vielfaches“ scheint bereits im Unterricht genannt worden und zumindest einigen Kindern bekannt zu sein, da der Versuch von Vahit, die Abkürzung kgV auszuformulieren, in <7> dem korrekten Fachterminus[3]des mathematischen Begriffs mit „kleiner gemeinsamer ver“ sehr nahe kommt. Mit der Bedeutung des kgV scheinen die Schülerinnen und Schüler jedoch noch nicht vertraut, denn Frau Teichmann sagt zu Beginn in <1> „warum machen wir das mit diesem ... kgV\ hab ich so genau noch gar nicht erklärt was das ist“. Es wäre somit zu erwarten, dass im Folgenden inhaltliche Konzepte des Begriffs und seiner Bedeutung inhaltlich thematisiert werden. Im Verlauf der Einführung scheint es jedoch zu Missverständnissen zu kommen. An der Sequenz mit Pelin und Nesrin lässt sich zeigen, dass einige der Kinder den Ausführungen der Lehrperson nur bedingt folgen können.
In <112> scheint die Lehrperson mit der Unterteilung der Kreise in Segmente, in <118> mit der Schraffierung eines der Segmente sowie in <128> mit der Frage: „..da steht ne Aufgabe, Pelin da wie heißt die Aufgabe“ verstärkt auf die Addition von zwei Brüchen abzuzielen. Dieses scheint zumindest einer der Schüler ähnlich zu verstehen und sagt in <123> „ein Drittel plus ein Viertel“. Pelin und Nesrin scheinen die Situation jedoch anders zu deuten. So scheint Pelin in <129> mit der Antwort „eins plus eins“ auf die zwei Kreise bzw. Kreissegmente verbunden mit einem Additionszeichen zu fokussieren und deutet dieses anscheinend als Aufgabe. Hieraufhin wird Nesrin von der Lehrperson in <130–131> aufgefordert zu antworten, da die Lehrperson mit der Lösung von Pelin unzufrieden scheint. Nesrin gibt nun die Lösung der von Pelin aufgestellten Aufgabe in <133> mit „zwei“ an. Als die Lehrperson hierauf eher mit Unverständnis reagiert, bessert Nesrin nach und sagt in <135> „eins“. Hier ergibt sich eine Vielzahl von Deutungsmöglichkeiten. Eine denkbare Möglichkeit wäre, dass Nesrin nach der gängigen ‚Taktik‘ der minimalen Veränderung agiert. Ist zwei im Mathematikunterricht nicht die richtige Lösung, man jedoch davon ausgeht, eigentlich alles richtig zu machen, ist es naheliegend, dass eins oder drei als richtige Lösungen in Frage kommen könnte. Es lässt sich jedoch nicht rekonstruieren, dass Nesrin den ursprünglichen Deutungsrahmen ihrer Antworten verlässt. Die Lehrperson reagiert hierauf in <136> mit „nee eins ist das Ganze“, was verdeutlicht, dass auch sie an ihrer Rahmung festhält: Sie deutet die Antworten anscheinend weiterhin vor der Rahmung der Bruchrechnung. In diesem Stil lässt sich auch der Rest der Szene deuten. Die Lehrperson deutet die Aussagen der Schülerinnen und Schüler vor dem Konzept des kgV oder der Bruchrechnung und die Schülerinnen und Schüler die Aussagen der Lehrperson allenfalls vor dem der Addition der Anzahl von Kreisen oder Kreissegmenten im Zahlbereich der Natürlichen Zahlen. Demnach bleibt die Rahmung der Lehrperson hier implizit verborgen und es wird auch nicht explizit im Unterrichtsdiskurs von der Lehrperson aufgegriffen, welche Deutung oder Bedeutungskonstruktion Pelin und Nesrin vornehmen.
Wie lässt sich dieses Vorgehen der Lehrpersonen in Bezug auf obige theoretische Ansätze beschreiben?
Bei der Einführung neuer mathematischer Begriffe lässt sich in Bezug auf das mathematisch-fachsprachliche Register rekonstruieren, dass die Bedeutungen der Begriffe sowie inhaltliche Bezüge zwischen den neuen mathematischen Begriffen und zu bereits bekannten alltagssprachlichen Begrifflichkeiten nicht oder nur implizit von der Lehrperson hergestellt werden. Bei der Einführung werden zu keinem Zeitpunkt die mathematischen Begriffe Nenner, Zähler, Bruch, Bruchstrich oder Vielfache verbal inhaltlich im offiziellen Unterrichtsgespräch geklärt. Ihre Bedeutungen bleiben implizit und werden unreflektiert in bekannte Rechenroutinen integriert. Vor allem wird der für die Lehrperson anscheinend offensichtliche Wechsel der Zahlbereiche von der Lehrperson nicht zum Lerngegenstand gemacht, wodurch ein Angleichen der Deutungen der Beteiligten nicht möglich erscheint. Das von Pimm (1987) formulierte Ziel, dass Schülerinnen und Schüler lernen sollten, wie ein native speaker der Mathematik zu sprechen, wird so schwer zu erreichen sein, denn der native speaker der Mathematik – die Lehrperson – lebt dieses aktive Sprechen nicht vor und thematisiert nicht explizit die mathematischen Konzepte/Rahmungen, die sich hinter ihren Deutungen verbergen.
Ein ähnliches Bild zeigt sich darin, wie die Lehrperson auf Besonderheiten im formalsprachlichen Register eingeht. Die Lehrperson achtet lediglich darauf, dass der richtige Artikel vor kgV gesetzt wird und das die Abkürzung des neuen mathematischen Begriffs sprachlich ausformuliert wird. Hierdurch soll anscheinend der Tatsache Rechnung getragen werden, dass ein hoher Anteil der Schulkinder nicht Deutsch als Muttersprache aufweist. Tiefergreifende sprachliche Zusammenhänge werden jedoch nicht geklärt. So weist die Lehrperson nicht darauf hin, welche bedeutungstragenden Bestandteile (klein, gemeinsam, Vielfache) den mathematischen Begriff prägen. Aber nur aufgrund der Tatsache, dass zwei der bedeutungstragenden Bestandteile des Begriffs „kleinstes gemeinsames Vielfaches“ alltägliche Begriffe darstellen und alle Kinder mit den Begriffen „klein“ und „gemeinsam“ im alltagssprachlichen Register handeln können werden, ergibt sich mitnichten die Bedeutung des Begriffs kgV im mathematische fachsprachlichen Register. Bildungssprachliche Kompetenzen werden in dieser Art des Unterrichts somit nicht vermittelt.
Nach der Analyse – bezogen auf das mathematisch-fachsprachliche Register – scheint eine mögliche Erklärung für die Missverständnisse bei der Einführung der neuen Begriffe naheliegend und gegebenenfalls ohne die extensive sequentielle Analyse der Interaktion auch einleuchtend. Die Kinder können aufgrund von (bildungs-) sprachlichen Defiziten den Ausführungen der Lehrperson nur eingeschränkt folgen und haben so Schwierigkeiten, im mathematischen Register sprachlich zu handeln. Dies wird ihre zukünftigen Defizite bezogen auf das mathematische und formalsprachliche Register verstärken und so zu einer ungünstig verlaufenden Entwicklung für zukünftige Bedeutungskonstruktionen führen. Verstärkt würde dieser Eindruck dann dadurch, dass die Lehrperson trotz der Einführung eines neuen mathematischen Begriffs Bemühungen vermissen lässt, explizit die Entwicklung eines fachsprachlichen bzw. formalsprachlichen Registers positiv zu unterstützen.
In diesem Sinne ließe sich die Szene sicherlich analysieren und die Missverständnisse der Lernenden erklären. Greifen wir jedoch auf obige Ansätze von Krummheuer (1992) zurück, lassen sich mit zusätzlichem Bezug zu Aukermann (2007) auch andere Erklärungen finden, die nicht rein auf sprachliche Defizite der Lernenden und auf die mangelnde Berücksichtigung dieser Defizite im Unterricht zurückzuführen sind. So lässt sich in der ausgewählten Sequenz rekonstruieren, dass die Lehrperson die Aufgabe oder Zeichnung an der Tafel auf der Grundlage ihrer fachlichen Ausbildung vor dem Konzept der Addition von rationalen Zahlen zu ‚rahmen‘ scheint und insofern eine Unterteilung eines Kreises mit der Markierung einiger dieser Teilflächen als Schaubild für einen Bruch ansieht. Es lassen sich des Weiteren Rahmungsdifferenzen unter den Schülerinnen und Schülern als auch zwischen diesen und der Lehrperson rekonstruieren. Die einen, wie z. B. Pelin und Nesrin (<129–141>), scheinen die Kreise wie Formen zu betrachten und diese in gängiger Weise auf der Grundlage einer Rahmung der Addition natürlicher Zahlen zu addieren. Einzig Otto scheint die Aufgabe ähnlich zu ‚rahmen’ wie die Lehrperson (<144>). Durch das implizite Vorgehen in den Handlungen der Lehrperson und dadurch, dass diese sich nicht vergewissert, auf Grundlage welcher Rahmung die Schülerinnen und Schüler die Aufgabe deuten, werden die unterschiedlichen Rahmungen der Aufgabe und die daraus resultierenden unterschiedlichen individuellen Situationsdefinitionen der Beteiligten nicht thematisiert. So greift die Lehrperson Nesrins Deutungen nicht auf, wodurch sie die Chance vergibt, die Rahmungsdifferenzen zwischen ihr und einem Großteil der Klasse zu koordinieren oder gar zu reduzieren. Hierdurch wird den Schülerinnen und Schülern nur schwer ermöglicht, ihre Situationsdefinitionen an jene von Otto und der Lehrperson anzunähern. Als Ergebnis zeigt sich, dass z. B. Pelin auch nach mehrfacher negativer Evaluation durch die Lehrperson zwar ihre Antworten wechselt, jedoch nie den Deutungsrahmen als Grundlage ihrer Antworten zu verlassen scheint. Die Deutung der Aufgabe auf der Grundlage einer Rahmung der Bruchrechnung scheint ihr verwehrt. Nach dieser Analyse sind die Missverständnisse nicht in den sprachlichen Defiziten der Kinder begründet, sondern eher in der fehlenden Interpretationskompetenz der Lehrperson, Rahmungsdifferenzen aller Beteiligter im Unterricht zu erkennen und zu koordinieren.
Eine solche Interaktionssituation bezeichnet Krummheuer als „übergangene Rahmungsdifferenz“ (Krummheuer 1992, S. 74 ff.). Mögliche Rahmungsalternativen der Schülerinnen und Schüler werden in dieser Interaktionssituation nicht thematisiert und schlicht übergangen. Das Ergebnis eines solchen Aushandlungsprozesses wird vielfach darin bestehen, dass ein Arbeitskonsens zwischen den Beteiligten nur zum Schein besteht, da die Lehrperson als Autorität in Bezug auf die Richtigkeit von Lerninhalten akzeptiert ist und diese sich nicht vergewissert, ob und wenn ja, welche Passung ihre Situationsdefinition mit denen der Kinder aufweist. Ein Effekt dieser Verschleierung von Rahmungsdifferenzen ist, dass die Interaktionssituationen den Eindruck eines einvernehmlichen Prozesses der Aushandlung von Bedeutung vermitteln – die Beteiligten jedoch nur scheinbar eine gemeinsam geteilt geltende Deutung in der kollektiven Argumentation des Unterrichts erreichen. Fragwürdig erscheint dieses Vorgehen aus mathematischer Sicht, da die fachliche Qualität solcher Verständigungsprozesse ‚ohne’ Verständigung zu bezweifeln ist, da eine Vielzahl der Beteiligten so kaum ein ähnliches Verständnis der Situation aufbauen können. Das Ergebnis des Aushandlungsprozesses unterliegt zudem einer gewissen Unbestimmtheit hinsichtlich dessen, was eigentlich ausgehandelt wurde und die mathematisch begründete Korrektheit wird einer „intersubjektiv erzielten Entlastung in einem Verständigungsprozess“ (Krummheuer 1992, S. 113) vorgezogen. Krummheuer spricht in diesem Fall davon, dass eine solche Form des Unterrichtens das Ziel der Plansollerfüllung über das Ziel eines verständnisorientierten Unterrichts stellt (Krummheuer 2004). Des Weiteren lässt sich aus interaktionistischer Sicht anmerken, dass bei dieser Verschleierung von Rahmungsdifferenzen zu erwarten ist, dass keine individuellen Deutungen hervorgebracht werden, welche die Fähigkeiten der Beteiligten überschreitet. Dies wird dazu führen, dass die ‚erzielte Verständigung’ keine Lernprozesse von nachhaltig Neuem über eine subjektive Überzeugtheit bei den Beteiligten evozieren wird.
Rekonstruktion einer Impliziten Pädagogik
Als zugrunde liegendes Strukturmerkmal bei der sprachlichen Gestaltung des Unterrichts lässt sich das Phänomen einer Implizitheit von Lerninhalten und des Vorgehens auf unterschiedlichen Ebenen rekonstruieren. Diese Implizitheit schlägt sich bei der Verwendung unterschiedlicher mathematisch-fachsprachlicher und formalsprachlicher Register nieder. Aber auch auf anderen Ebenen zeigt sich die Implizitheit des Vorgehens der Lehrperson. So lassen sich seitens der Lehrperson keine expliziten Vergewisserungen darüber rekonstruieren, auf Grundlage welcher Rahmung Antworten von Schülerinnen und Schülern zu deuten sind.
Ein solches Vorgehen bei der Einführung neuer mathematischer Begriffe lässt sich anhand eines theoretischen Konzepts erklären, das ich als Implizite Pädagogik (siehe Schütte 2009 S. 187 ff. und 2010 S. 212 ff.) bezeichne. Nach diesem besteht die Aufgabe von Lehrpersonen vorwiegend darin, Lernenden eine Lernumgebung bereitzustellen und innerhalb dieser zu begutachten, wie sich die angeborenen individuellen Fähigkeiten und ‚Talente‘ jedes einzelnen Kindes entwickeln. Die Implizite Pädagogik folgt demnach dem Grundgedanken, dass Schülerinnen und Schüler sich allein aufgrund ihrer mitgebrachten Fähigkeiten Bedeutungen selbstständig erschließen können oder sich zugrunde liegende inhaltliche und sprachliche Zusammenhänge und Strukturen für die Kinder ‚wie von selbst‘ ergeben. Hiernach verlieren der Unterricht bzw. die Qualifikation der Lehrenden den entscheidenden Einfluss auf einen möglichen Schulerfolg von Schülerinnen und Schülern. Bestehende soziale Verhältnisse in der Schülerschaft werden so reproduziert. Zudem lassen sich Unterschiede in den Leistungen zwischen Schülerinnen und Schülern so vorschnell als durch die Schule unveränderbar einstufen und anhand von sozioökonomischen, sozialen und individuell-kognitiven Unterschieden legitimieren.
Es stellt sich die Frage, ob sich in Bezug auf obige Überlegungen zum Lernen in unterschiedlichen Lernorten solche beschriebenen Phänomene nur beim Lernen in der (Grund-)Schule oder auch beim Lernen von Mathematik in der KiTa oder der Familie zeigen. Insofern wird im folgenden illustrierenden Beispiel eine Szene mit Kindern im Vorschulalter und einer betreuenden Person dahingehend analysiert, ob die sprachliche Gestaltung der Situation auch einer Impliziten Pädagogik zu folgen scheint.
Im folgenden Abschnitt werden Analyseergebnisse von Szenen aus dem Projekt erStMaL (early Steps in Mathematics Learning) des Frankfurter IDeA-Zentrums zur Komparation der obigen Analysen hinzugezogen. Zur Erforschung individueller Entwicklungs- und Lernprozesse von Kindern mit sogenannten Risikofaktoren haben das Deutsche Institut für Internationale Pädagogische Forschung (DIPF) und die Goethe-Universität das Forschungszentrum IDeA (Center for Research on Individual Development and Adaptive Education of Children at Risk) gegründet. In diesem Rahmen leitete Prof. Dr. Krummheuer zusammen mit Prof. Dr. Vogel und Jun.-Prof. Dr. Brandt das Projekt erStMaL (early Steps in Mathematical Learning; vgl. Brandt et al. 2011). Im Projekt erStMaL wird u. a. die Entwicklung einer sozial-konstruktivistisch orientierten Entwicklungstheorie mathematischen Denkens im Kindesalter angestrebt. Auf dieser theoretischen Basis werden so dann auch Untersuchungen zu Entwicklungen von Kindern mit spezifischen Risiken möglich. Hierzu ist eine Longitudinalstudie initiiert worden, in der Kinder im Alter zwischen drei und zehn Jahren in verschiedenen Gruppenzusammensetzungen (zwei bis vier Kinder) mit von Projektmitarbeitenden selbst entwickelten mathematischen Spiel- und Erkundungssituationen konfrontiert werden. Es wurden mit 144 Kindern im Frankfurter Raum sechs Erhebungen in circa halbjährlichen Abständen durchgeführt. Die Aufgabensituationen beziehen sich auf alle oben genannten mathematischen Kompetenzbereiche (vgl. Acar Bayraktar et al. 2011).[4]
Die Szene Tierpolonaise[5]
Im Folgenden wird ein Sequenzauszug der Szene „Tierpolonaise“[6] dargestellt. Beteiligt an der Situation sind Ayse (4;2 Jahre), die einzige Tochter eines türkisch-deutschen Paares, Kai (4;3 Jahre), der monolingual deutsch aufwächst sowie die Begleitperson B.

Die Spiel- und Erkundungssituation behandelt eine Fragestellung aus dem Bereich Kombinatorik. Sie ist in dem oben beschriebenen Projekt nach speziell ausgearbeiteten Designvorgaben geplant und durchgeführt worden. Die Kinder erhalten hiernach drei Tierfiguren, einen Elefanten, einen Tiger und einen Affen, und ein Zirkuspodest. Aufgabe der Kinder ist es, gemeinsam unterschiedliche Reihenfolgen zu finden, in denen die Tiere über das Podest laufen könnten und diese gegebenenfalls durch geschickte Strategien zu zählen. Des Weiteren konnten die Kinder die jeweiligen Positionen der Tiere in der Reihenfolge bestimmen.
Die Szene lässt sich in drei Teilsequenzen gliedern:
Es folgt das Transkript sowie die Analyse des dritten Abschnittes des Transkriptes.
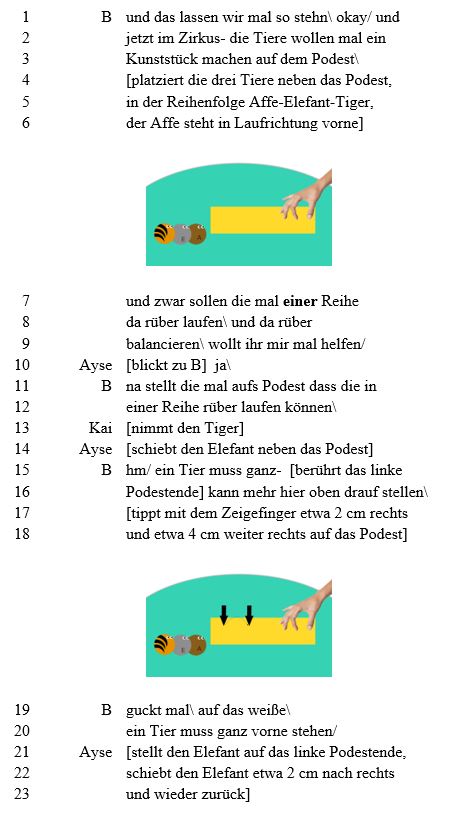



Analyse der sprachlichen Gestaltung der Szene
Den Kindern werden drei Tiere und ein Zirkuspodest zur Verfügung gestellt. Die Beteiligten erzeugen vier Permutationen, von denen die Entwicklung der folgenden drei Permutationen analysiert wird:
Permutation I wird von den Kindern gleichsam synchron erzeugt, nachdem die Betreuerin die Kinder auffordert, die Tiere in einer „Reihe“ <12> über das Zirkuspodest laufen zu lassen. Offen bleibt jedoch, wie der von der Lehrperson benutzte Begriff der Reihe gefasst werden kann: Soll hiermit die Art der Aufstellung, sich in eine Linie zu stellen oder die Rangordnung, z. B. von klein nach groß sortiert, ausgedrückt werden? In der Komparation mit obiger Szene aus dem Mathematikunterricht der Grundschule lässt sich in Bezug auf das (mathematisch)-fachsprachliche Register rekonstruieren, dass der Begriff Reihe nicht explizit von der Betreuerin inhaltlich geklärt wird. Im späteren Verlauf verwendet die Betreuerin den Begriff „Reihenfolge“ <62> anscheinend synonym zum Begriff Reihe. Da Ayse und Kai erst anfangen, die erste Permutation zu stellen, nachdem die Betreuerin relativ direktiv und durch starke Gestik unterstützt fordert, die Tiere in einer Reihenfolge über das Podest laufen zu lassen, ist davon auszugehen, dass die Kinder entweder die Situation anders deuten als die Lehrperson oder aber mit dem Begriff Reihe keine weiteren Handlungen in Verbindung bringen können. Es lässt sich jedoch rekonstruieren, dass die Betreuerin zumindest durch die gestischen Untermauerungen und durch das Bewegen der Tiere (<17–18>, <47–49> und <53–57>) anscheinend eine erste Vorstellung einer Reihenfolge bei den Kindern hervorzurufen versucht. Dieser Zusammenhang lässt sich jedoch nur für diejenigen erkennen, die das Konzept der Reihenfolge bereits beherrschen und ggf. wissen, dass hier auf unterschiedliche Permutationen durch die Bildung unterschiedlicher Reihenfolgen der Tiere abgezielt wird. Es ist davon auszugehen, dass dieser Zusammenhang für die Kinder weiterhin implizit verborgen bleibt und die gestischen und handelnden Unterstützungen nicht zur Klärung des Konzeptes der Reihenfolge beitragen werden.
Am Beispiel der ersten hervorgebrachten Permutation zeigt sich die Hervorbringung einer geteilt geltenden Deutung über die räumliche Orientierung von vorne und hinten, die sich in der konsistenten Laufrichtung der Tiere in allen noch zu behandelnden Fällen widerspiegelt. Diese ‚einvernehmliche’ Deutung scheint jedoch nicht auf einer gemeinsamen Rahmung über den zu erfüllenden Arbeitsauftrag der Beteiligten zu basieren. Die Kinder rahmen die Sequenz anscheinend vor alltäglichen Konzepten von vorne und hinten oder ggf. vor ersten mathematischen Konzepten zur Raumorientierung; die Betreuerin vor einem kombinatorischen Hintergrund und der Variierungen von Reihenfolgen zur Erlangungen unterschiedlicher Permutationen. Insofern scheint auch in dieser Sequenz – ähnlich wie in der Szene kgV – eine Rahmungsdifferenz vorzuliegen, und auch diese wird von der Betreuerin nicht koordiniert.
Auch das Aufstellen der zweiten Permutation bedarf deutlicher Unterstützung von der Betreuerin. Erst die konkrete Aufforderung, dass die Tiere sich ein weiteres Mal „hinten anstellen“ <66> müssten und die Frage, welches Tier diesmal „ganz vorne“ <68> stehen soll, führt dazu, dass die beiden Kinder sich je ein Tier nehmen und beginnen, die Reihenfolge zu stellen. Ebenso wenig wie bei der ersten Permutation wird hier der Begriff der Reihe oder Reihenfolge inhaltlich differenziert.
Permutation III stellt dagegen eine Einzelleistung von Kai dar. Der Handlungsvollzug erscheint flüssig und auch seine sprachliche Intonation weist darauf hin, dass er einen ihm offensichtlich klaren Handlungsplan umsetzt. Er nennt den Tiger einen Löwen <114>, was die Deutung stützt, dass die Spezifität der einzelnen Tierarten für ihn nicht weiter von Bedeutung zu sein scheint. Dies könnte ein erstes Indiz für eine mögliche Modulation zu einer stärker mathematischen Rahmung der Situation sein. Er würde hiernach seine alltägliche Rahmung der Situation partiell verlassen und die Tiere als Elemente, die es unterschiedlich anzuordnen gilt, betrachten.
Als gemeinsames zugrunde liegendes Strukturmerkmal bei der sprachlichen Gestaltung der vorliegenden Lernumgebung durch die Betreuerin lässt sich auch in dieser Szene das Phänomen einer Implizitheit von Lerninhalten rekonstruieren. Die Implizitheit beim Vorgehen der Lehrperson schlägt sich wie oben beschrieben auf das Erlernen mathematisch-fachsprachlicher und formalsprachlicher Register der Kinder nieder. Sie wird mit gewissen Abstrichen auch bei der Koordinierung unterschiedlicher Rahmungen deutlich, wobei hier die gestischen Untermauerungen und das Bewegen der Tiere durch die Betreuerin als ein erster Versuch gewertet werden könnten, unterschiedliche Rahmungen der Beteiligten zu koordinieren. Stützen lässt sich diese Deutung dadurch, dass dieser Versuch zu einer als geteilt geltenden Deutung von vorne und hinten zwischen den Beteiligten führt. Eine sprachliche Koordination der unterschiedlichen Rahmungen durch die Betreuerin findet sich jedoch nicht.
Betrachtet man die beiden Analysen über die unterschiedlichen Lernorte und Altersspannen hinweg, lassen sich auf struktureller Ebene Ergebnisse festhalten, die sich konsistent mit dem theoretischen Konzept der Impliziten Pädagogik beschreiben lassen (Schütte 2009). In den analysierten Szenen handeln die Betreuenden nicht als sprachliche Vorbilder. Das bedeutet, dass die Lehrperson in der Szene kgV weder Begriffe noch die bedeutungstragenden Bestandteile dieses Begriffes im offiziellen Unterrichtsgespräch thematisch klärt und/oder diese selbst in zusammenhängenden Sätzen verwendet und so den sprachlichen Gebrauch mit diesen vorlebt und schult. Ähnlich verhält sich dieses bei der Betreuerin in der Szene „Tierpolonaise“. Hier lässt sich die Betreuerin jedoch teilweise auf nonverbaler Ebene als sprachliches Vorbild ausmachen, da sie die Kinder beim Finden von Reihenfolgen gestisch unterstützt. Diese Handlungen begleitet sie jedoch nicht verbal mündlich, wodurch die Kinder Schwierigkeiten haben, den darauf folgenden verbalen mündlichen Auftrag, eine weitere Permutationen zu finden, zu verstehen und diesen vorerst nicht bearbeiten können. Insofern scheint hier mit Einschränkungen ein sprachliches Vorbild durch die Begleitperson vorzuliegen, jedoch keines in Bezug auf die Verbindung von verbal-mündlichem und gestischem Lernen, sondern lediglich auf gestischer Ebene. Hierdurch können die Kinder nicht im Sinne des Lernens mit Format (zum Begriff vgl. Bruner 2002, S. 103 und Krummheuer 1992, S. 140) an einer in der Interaktion fortgeschrittenen Person sprachlich wachsen, indem sie zunehmend Autonomie durch die Übernahme verbaler Handlungsschritte von der in der kollektiven Argumentation fortgeschrittenen Person gewinnen können. In solchen Lernsituationen mag es nach obigen Ansätzen, die in Anlehnung an Hallidays Registeransatz zu verstehen sind und auf mangelnden Fähigkeiten von Kindern fokussieren, nicht verwundern, dass es gerade bei Kindern, die bildungsfern oder mehrsprachig aufwachsen, zu Verständnisproblemen über die Unterrichtsinhalte kommen kann. Dieses ließe sich auch in den vorliegenden Szenen vermuten. Die sprachlichen Defizite von Pelin und Nesrin in der ersten Szene und von Ayse in der zweiten Szene wären hiernach die Ursachen für ihr Missverstehen und für die daraus resultierenden mangelnden Fähigkeiten, die mathematischen Aufträge adäquat umzusetzen. Dies alles würde im Einklang zur gängigen Diskussion über mangelnde sprachliche Fähigkeiten von Kindern in der Schule passen – vor allem von denen, die in mehr als einer Sprache leben und lernen. Eine Lösung dieses Problems wäre eine Schulung der sprachlichen Fähigkeiten der Kinder und damit das Beheben ihrer Defizite. So weit – so gut. Aber wie sich in den vorherigen Analysen zeigt, greift dieser Weg nur vordergründig.
So wurde oben aufgezeigt, dass dieses beschriebene Missverstehen der Kinder auf unterschiedliche Deutungen der Situationen aufgrund von unterschiedlichen Rahmungen der Beteiligten zurückführen ist (vgl. hierzu Aukermann 2007). Ob hierzu sprachliche Probleme bei den beteiligten Kindern einen zusätzlich erschwerenden Faktor darstellen, darüber kann lediglich gemutmaßt werden. Bezeichnender Weise lassen sich die unterschiedlichen Rahmungen der Situationen, z. B. in der zweiten Szene, jedoch nicht nur bei den Kindern mit vermeintlich sprachlichen Defiziten rekonstruieren, sondern auch bei Kai, der monolingual deutsch und nicht bildungsfern aufwächst. Er und Ayse scheinen die Situation ähnlich und somit auch ‚ähnlicher anders’ als die Betreuerin zu rahmen. Insofern lässt sich die Hypothese aufstellen, dass Rahmungen von Kindern mit deutlich unterschiedlichen sprachlichen Fähigkeiten trotzdem sehr nahe beieinanderliegen können und Kinder ohne sprachliche Defizite eventuell ebenso große Rahmungsdifferenzen zu den Rahmungen der Lehrpersonen aufbauen können. Das bedeutet, dass hier die ausschließliche Perspektive auf die möglichen sprachlichen Defizite der Kinder zu kurz greift. Sicherlich ist es für alle beteiligten Kinder wünschenswert, wenn sie sowohl in formalsprachliche als auch mathematisch-fachsprachliche Aspekte eingeführt werden bzw. worden sind und die Lehrperson diesen Prozess bestmöglich als sprachliches Vorbild begleitet. Aber auch, wenn Kinder ein sprachliches Vorbild haben, benötigen sie eine Lehrperson, die sich auf ihre Deutungen einlässt und die zugrundeliegenden Rahmungen aller Beteiligter zu modulieren versucht. So sieht man in der Szene „Tierpolonaise“, dass sich eine Annäherung der Rahmungen von Betreuerin und Kai ausmachen lässt. Hierbei ist es durchaus möglich, dass Kais sprachliche Fähigkeiten diesen Prozess begünstigen. Diese Modulation müsste jedoch nun von der Betreuerin so koordiniert werden, dass auch Ayse von Kais erstem Schritt, seine Deutung mit der Deutung der Betreuerin zu einer stärkeren Passung zu bringen, profitieren kann. Ohne eine solche Modulierung von Rahmungen ist es zwar möglich, dass eine gemeinsam geteilt geltende Deutung der Situation, wie vorliegend über ‚vorne und hinten’, zwischen den Beteiligten ausgehandelt wird. Mit Verweis auf Krummheuer (1992, S. 44 f.) ist hier im Sinne einer lerntheoretischen Betrachtung aber einzuschränken, dass Lernen erst als eine Neukonstruktion oder ‚Umkonstruktion’ von hinter den Situationsdefinitionen liegenden Rahmungen zu verstehen ist, die in späteren Szenen zur Herstellung von Situationsdefinitionen und gemeinsam geteilt geltenden Deutungen erneut aktiviert werden könnten. Da die Rahmungen in vorliegender Situation jedoch nicht koordiniert werden, lediglich die Situationsdefinitionen vordergründig zur Passung zu kommen scheinen, ist nicht von einem Lerneffekt der Beteiligten auszugehen, der über die jeweilige Situation der Beteiligten trägt. Einschränkend ist hierbei zu erwähnen, dass diese Ausführungen sich auf die Rahmungsdifferenz zwischen der Deutung der Begleitperson und ihrer stochastischen Rahmung der Situation und den Kindern und ihrer vornehmlich raumgeometrischen Rahmung der Situation beziehen. Sehr wohl könnte man überlegen, ob die Kinder gegebenenfalls ihre raumgeometrische Rahmung durch ihre gemeinsam geteilt geltende Deutung zu vorne und hinten modifizieren und diese in zukünftigen raumgeometrischen Situation erneut aktivieren können, wodurch für sie zwar kein Lerneffekt im Bereich der Kombinatorik, wie mit der Situation intendiert, wohl aber im Bereich der Geometrie erzielt worden wäre.
Aufgrund der nicht wegzudenkenden bzw. wegzuredenden Vielfältigkeit der Schülerschaft in deutschen Schulen, die durch aktuelle Themen wie eine flächendeckende Umsetzung inklusiven Unterrichts oder durch die jüngste, verstärkte Migration von Flüchtlingen, zwar an Aktualität zu gewinnen scheint, in der Sache jedoch nicht neu ist, kann und wird es an allen Lernorten zu einer Vielzahl unterschiedlicher Deutungen in Bedeutungsaushandlungen fachlichen Lernens kommen. Die hierbei zugrundeliegenden Rahmungen der Kinder werden ggf. trotz ihrer Vielfältigkeit mehr Passung zueinander haben als zu den Rahmungen der Lehrenden. So werden die Rahmungen der Kinder, die einem zumindest teilweise geteilten Alltag entspringen, ohne Koordinierung kaum eine Passung zu der fachlich geprägten Rahmung der Lehrpersonen oder anderer pädagogisch betreuenden Personen aufweisen. Ziel sollte es somit sein, Lehrpersonen sowie Erzieherinnen und Erzieher zunächst für vielfältigen Deutungsmöglichkeiten der Inhalte in (mathematischen) Lernsituationen zu sensibilisieren. Hierauf aufbauend sollten Lehrende eine Interpretationskompetenz entwickeln, um unterschiedliche Deutungen aufgrund von Rahmungsdifferenzen, die den Motor des Lernens darstellen, zu erkennen und diese beim Lernen zu thematisieren, und erzeugen somit die Möglichkeit zu einer Modulation von Rahmungen bei den Lernenden.
Acar Bayraktar, E., Hümmer, A.-M., Huth, M., Münz, M., & Reimann, M. (2011). Forschungsmethodischer Rahmen der Projekte erStMaL und MaKreKi. In B. Brandt, R. Vogel & G. Krummheuer (Eds.), Mathematikdidaktische Forschung am ‘Center for Individual Development and Adaptive Education’. Grundlagen und erste Ergebnisse der Projekte erStMaL und MaKreKi (Volume 1, pp. 11–24). Münster: Waxmann.
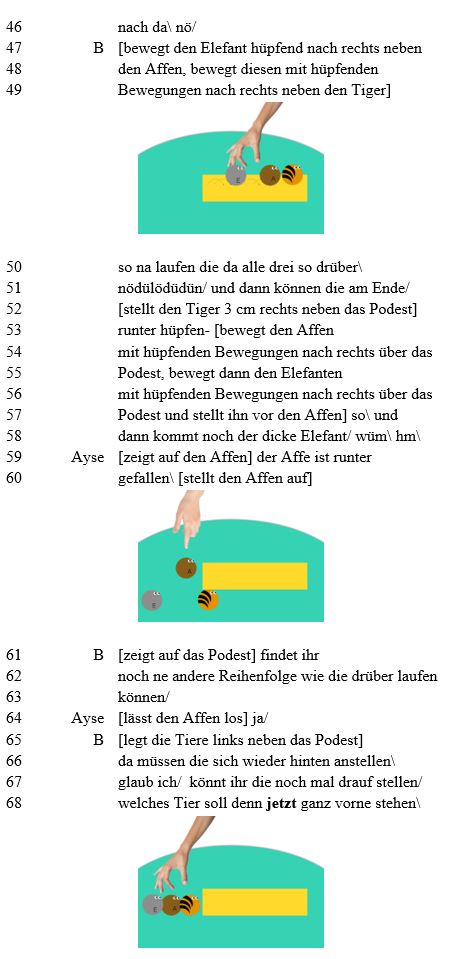
Aukermann, M. (2007). A culpable CALP: rethinking the conversational/academic language proficiency distinction in early literacy instruction. The Reading Teacher, 60(7), 626–635.
Brandt, B., Vogel, R., Krummheuer, G. 2011. Mathematikdidaktische Forschung am "Center for Individual Development and Adaptive Education". Grundlagen und erste Ergebnisse der Projekte erStMaL und MaKreKi (Bd. 1) (Vol. 1). Münster, New York, München, Berlin: Waxmann.
Bruner, J. (2002). Wie das Kind sprechen lernt. Bern: Huber. [im Original erschienen als: Bruner, J. (1983). Child’s talk: Learning to use language. New York: Norton.]
Cummins, J. (2000). Language, Power and Pedagogy: Bilingual children in the crossfire.Clevedon: Multilingual Matters.
Deutsches PISA-Konsortium (2004). PISA 2003: Der Bildungsstand der Jugendlichen in Deutschland. Ergebnisse des zweiten internationalen Vergleichs. Münster: Waxmann.
Fthenakis, W. E. (2009): Natur-Wissenschaften 2. Frühe mathematische Bildung. Troisdorf: Bildungsverlag Eins.
Gee, J. P. (1999). An introduction to discourse analysis. Theory and method. London and New York: Routledge.
Goffman, E. (1974): Frame analysis. An essay on the organisation of experience. Cambridge: Harvard University Press.
Goffmann, E. (1959). The presentation of self in everyday life. New York: Doubleday.
Gogolin, I. (1994): Der monolinguale Habitus der multilingualen Schule. Münster und New York: Waxmann.
Gogolin, I. (2006). Bilingualität und die Bildungssprache der Schule. In P. Mecheril & T. Quehl (Eds.), Die Macht der Sprachen. Englische Perspektiven auf die mehrsprachige Schule (pp. 79–85). Münster: Waxmann.
Gogolin, I., & Roth, H.-J. (2007). Bilinguale Grundschule: Ein Beitrag zur Förderung der Mehrsprachigkeit. In T. Anstatt (Ed.), Mehrsprachigkeit bei Kindern und Erwachsenen. Erwerb, Formen, Förderung (pp. 31–45). Tübingen: Narr Francke Attempo Verlag.
Halliday, M. A. K. (1975). Some aspects of sociolinguistics. In UNESCO (Ed.), Interactions between linguistics and mathematical education (pp. 64–73). Kopenhagen: UNESCO.
Heinze, A., & Rudolph-Albert, F. (2008). Mathematische Kompetenzentwicklung und Sprachfähigkeit bei Schülerinnen und Schülern mit Migrationshintergrund in der Grundschule. In E. Vasarhélyi (Ed.), Beiträge zum Mathematikunterricht 2008 (pp. 669–672). Münster: WTM-Verlag.
Heinze, A., Herwartz-Emden, L., Braun, C. & Reiss, K. (2011). Die Rolle von Kenntnissen der Unterrichtssprache beim Mathematiklernen. Ergebnisse einer quantitativen Längsschnittstudie in der Grundschule. In Prediger, S. & Özdil, E. (Hrsg.): Mathematiklernen unter Bedingungen der Mehrsprachigkeit – Stand und Perspektiven der Forschung und Entwicklung in Deutschland (S. 11-33). Münster: Waxmann.
Huth, M. (2011): Das Zusammenspiel von Gestik und Lautsprache in mathematischen Gesprächen von Kindern. In B. Brandt, G. Krummheuer & R. Vogel (Hg.): Die Pro- jekte erStMaL und MaKreKi, Mathematikdidaktische Forschung am “Centre for In- dividual Development and Adaptive Education” (IDeA). Münster: Waxmann, 197- 244.
Kultusministerkonferenz (2004): Bildungsstandards im Fach Mathematik für den Primarbereich. Luchterhand, Darmstadt.
Krummheuer, G. (2013). The relationship between diagrammatic argumentation and narrative argumentation in the context of the development of mathematical thinking in the early years. Educational Studies in Mathematics:, 84(2), 249 – 265.
Krummheuer, G. (2004): Wie kann man Mathematikunterricht verändern? Innovation von Unterricht aus Sicht eines Ansatzes der Interpretativen Unterrichtsforschung. In: Journal für Mathematik-Didaktik, 25, H.2, 112-129.
Krummheuer, G. (1992). Lernen mit »Format«. Elemente einer interaktionistischen Lerntheorie. Diskutiert an Beispielen mathematischen Unterrichts. Weinheim: Deutscher Studien Verlag.
Krummheuer, G., & Brandt, B. (2001). Paraphrase und Traduktion. Partizipationstheoretische Elemente einer Interaktionstheorie des Mathematiklernens in der Grundschule. Weinheim: Beltz.
Meyer, M., & Prediger, S. (2011). The use of first language Turkish as a resource. A German case study on chances and limits for building conceptual understanding. In M. Setati, T. Nkambule and L. Goosen (Eds.), Proceedings of the ICMI Study 21 Mathematics and language diversity (pp. 225–234). Sao Paulo: ICMI.
Moschkovich, J. (2002). A situated and socialcultural perspective on bilingual mathematics learners. Mathematical Thinking and Learning, 4(2&3), 189–212.
OECD (Ed.) (2005). School factors related to quality and equity. OECD Publishing.
OECD (Ed.) (2006). Where immigrant students succeed. A comparative review of performance and engagement in PISA 2003. OECD Publishing.
van Oers, B. (1997). The narrative nature of young children's iconic representations: some evidence and implications. International Journal of Early Years Education. 1997, vol. 5, nr 3, 237-246.
Pimm, D. (1987). Speaking mathematically. London: Routledge.
Riebling, L. (2013). Sprachbildung im naturwissenschaftlichen Unterricht. Interkulturelle Bildungsforschung (Volume 20). Münster: Waxmann.
Schreiber, C. (2010). Semiotische Prozess-Karten. Chatbasierte Inskriptionen in mathematischen Problemlöseprozessen (Vol. 4). Münster, New York, München, Berlin: Waxmann.
Schütte, M. (2009). Sprache und Interaktion im Mathematikunterricht der Grundschule. Zur Problematik einer Impliziten Pädagogik für schulisches Lernen im Kontext sprachlich-kultureller Pluralität. Münster: Waxmann.
Schütte, M. (2010). Implizite Pädagogik – Eine Barriere für Lernen im Mathematikunterricht der Grundschule. In B. Brandt, M. Fetzer & M. Schütte (Eds.), Auf den Spuren Interpretativer Unterrichtsforschung (pp. 209–242). Münster: Waxmann.
Schütte, M., & Kaiser, G. (2011). Equity and the quality of the language used in mathematics education. In B. Atweh, M. Graven, W. Secada & P. Valero (Eds.), Mapping equity and quality in mathematics education (pp. 237–251). New York: Springer.
Stanat, P., Pant, H. A., Böhme, K. und Richter, D. (2012): Kompetenzen von Schülerinnen und Schülern am Ende der vierten Jahrgangsstufe in den Fächern Deutsch und Mathematik: Ergebnisse des IQB-Ländervergleichs 2011. Münster und New York: Waxmann.
Strauss, A., & Corbin, J. (1996). Grounded Theory. Grundlagen Qualitativer Sozialforschung. Weinheim: Beltz Psychologie Verlags Union.
Tiedemann, K. (2012). Mathematik in der Familie. Zur familialen Unterstützung früher mathematischer Lernprozesse in Vorlese- und Spielsituationen. Münster: Waxmann.
Voet Camelli, B. (2008): Vorschulische Sprachförderung für Kinder mit Migrationshintergrund vor dem Überang zwischen Kindergarten und Grundschule am Beispiel der hessischen Vorlaufkurse
Voigt, J. (1984). Interaktionsmuster und Routinen im Mathematikunterricht. Theoretische Grundlagen und mikroethnographische Fallunterscheidungen. Weinheim: Beltz Verlag.
Zevenbergen, R. (2001). Language, social class, and underachievement in school mathematics. In P. Gates (Ed.), Issues in mathematics teaching (pp. 38–50). New York: Routledge.

[3] In diesem Artikel wird mit Fachterminus die Bezeichnung eines mathematischen Begriffs definiert. Die Bezeichnung des mathematischen Begriffs zusammen mit den hinter der Bezeichnung stehenden mathematischen Bedeutungen wird im Weiteren durch den Ausdruck Begriff symbolisiert.
[4] Weitere Informationen zum Projekt erStMaL sowie Informationen über alle Qualifikationsarbeiten und Mitarbeiter des Projektes erhalten Sie unter: http://www.idea-frankfurt.eu/wissen/projekte/projekt-erstmal und in Brandt et al. 2011).
[5] Eine ausführliche Analyse der Szene findet sich in Schütte 2014.
[6] Die hier vorliegende Situation wurde von Melanie Huth für ihr Dissertationsvorhaben entwickelt und im Projekt erStMal angewendet (vgl. Huth 2011)